第五版年底出版,目前暂停更新
主要参考书籍为Shumway和Stoffer(2017)的Time Series Analysis and Its Applications: With R Examples。
该书第五版正在制作,配套astsa包中的部分数据集会逐渐更新,所以后期也许会换成第五版内容。
该内容为学习笔记,会很碎片化,同时参考了作者在github上给出的代码。
提示框表明这部分完全是个人理解,可能有误。
一切错误和想讨论的内容欢迎联系邮箱(zhoubolin0404@126.com),感谢!
在本章中,我们将介绍时间序列背景下的经典多元线性回归、模型选择、非平稳时间序列预处理(如趋势去除)的探索性数据分析、差分(differencing)和后移算子(backshift operator)的概念、方差稳定和时间序列的非参数平滑。
1 时间序列背景下的经典回归
对于时间序列\(x_t\)(\(t=1,\cdots,n\)),受到一组可能的输入或自变量序列(\(z_{t1},z_{t2},\cdots,z_{tq}\))的影响。用线性回归模型来考虑这种关系,则模型为:
\[ x_t=\beta_0+\beta_1z_{t1}+\beta_2z_{t2}+\cdots+\beta_qz_{tq}+w_t \]
其中\(\beta_0,\beta_1,\cdots,\beta_q\)是固定的回归系数,\(w_t\)是随机误差或噪声过程,均值为\(0\),方差为\(\sigma_w^2\),正态分布。
\(z_{t}\)一般就是时间。
1.1 简单线性回归
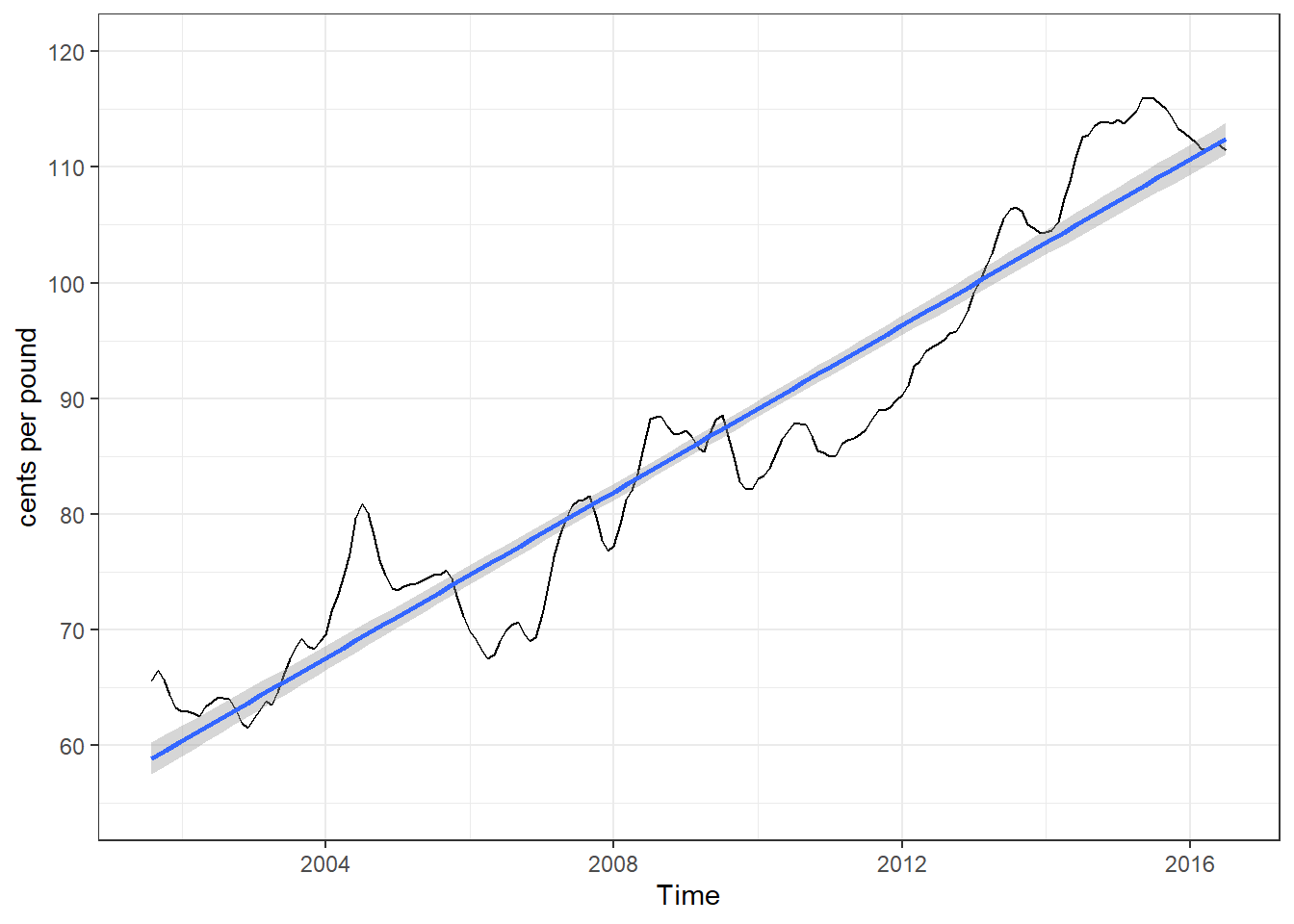
图 1展示了2001年8月到2016年7月美国某码头鸡肉每月价格,直线是线性回归的拟合。

拟合模型为:
\[ x_t=\beta_0+\beta_1z_t+w_t,\ z_t=2001\frac{7}{12},2001\frac{8}{12},\cdots,2016\frac{6}{12} \]
其中\(w_t\)被假设为一个独立同分布的正态分布序列(如不成立需要进行额外操作,第三章会介绍)。
没看懂为什么是\(2001\frac{7}{12}\)到\(2016\frac{6}{12}\)。
之后是对一元线性回归的计算,再后面是多元的,方法类似,故不对一元的进行解释,直接给出结果。
summary(fit <- lm(chicken ~ time(chicken), na.action = NULL))
Call:
lm(formula = chicken ~ time(chicken), na.action = NULL)
Residuals:
Min 1Q Median 3Q Max
-8.7411 -3.4730 0.8251 2.7738 11.5804
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7131.02247 162.41335 -43.91 <2e-16 ***
time(chicken) 3.59211 0.08084 44.43 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.696 on 178 degrees of freedom
Multiple R-squared: 0.9173, Adjusted R-squared: 0.9168
F-statistic: 1974 on 1 and 178 DF, p-value: < 2.2e-16结果表明:斜率系数\(\hat\beta_1=3.59\)(标准误差为\(0.08\)),\(p<0.001\),结果显著。
接下来会论述多元线性回归的计算过程,方便引出Akaike信息准则(Akaike’s Information Criterion,AIC),个人感觉不知道怎么推导也没什么问题。仅从个人理解角度进行概括,看不懂可以跳过,或者给出修改建议。
1.2 多元线性回归
多元线性回归模型,\(z_t=(z_{t1},\ z_{t2},\ \cdots,\ z_{tq})'\)和\(\beta=(\beta_0,\ \beta_1,\ \cdots,\ \beta_q)'\)这种列向量表示起来更为方便。
模型可以表示为:
\[ x_t=\beta_0+\beta_1z_{t1}+\beta_2z_{t2}+\cdots+\beta_qz_{tq}+w_t=\beta'z_t+w_t \]
其中\(w_t\sim\operatorname{iid\ N}(0,\ \sigma_w^2)\)。
普通最小二乘法(Ordinary Least Square,OLS)下,最小化的误差平方和(residual sum of squares或sum of squares for error,RSS或SSE)为:
\[ Q=\sum_{t=1}^{n}w_t^2=\sum_{t=1}^{n}(x_t-\beta'z_t)^2 \]
最小化(\(Q\)关于\(\beta\)的偏导数为0)需要满足\(\sum_{t=1}^n(x_t-\hat\beta'z_t)z_t'=0\)(表示\(w_t\)和\(z_t\)不相关),得到正规方程(normal equations):
\[ (\sum_{t=1}^{n}z_tz_t')\hat\beta=\sum_{t=1}^{n}z_tx_t \]
对这个方程求解就可以得到:
\[ \hat\beta=(\sum_{t=1}^{n}z_tz_t')^{-1}\sum_{t=1}^{n}z_tx_t \]
所以最小化的误差平方和为:
\[ \operatorname{SSE}=\sum_{t=1}^{n}(x_t-\hat\beta'z_t)^2 \]
这是无偏的(\(\operatorname{E}(\hat\beta)=\beta\)),且具有最小方差。
如果误差\(w_t\)是正态分布,\(\hat\beta\)是\(\beta\)的最大似然估计,且具有正态分布
\[ \operatorname{cov}(\hat\beta)=\sigma_w^2C \]
其中
\[ C=(\sum_{t=1}^{n}z_tz_t')^{-1} \]
\(C\)是\(z_t\)的协方差矩阵的逆。
方差\(\sigma_w^2\)的无偏估计是
\[ s_w^2=\operatorname{MSE}=\frac{\operatorname{SSE}}{n-(q+1)} \]
\(\operatorname{SSE}\)表示均方误差(mean squared error)。正态假设下
\[ t=\frac{(\hat\beta_i-\beta_i)}{s_w\sqrt{c_{ii}}} \]
服从自由度为\(n-(q+1)\)的\(t\)分布,\(c_{ii}\)表示矩阵\(C\)的第\(i\)个对角线元素。对于\(i=1,\ \cdots,\ q\),该结果常用于检验零假设\(\operatorname{H_0}:\beta_t=0\).
竞争模型关注隔离或选择最佳自变量子集点。选择\(r<q\)个独立模型,即\(z_{t,1:r}={z_{t1},\ z_{t2},\ \cdots,\ z_{tr}}\)。模型为
\[ x_t=\beta_0+\beta_1z_{t1}+\cdots+\beta_rz_{tr}+w_t \]
零假设为\(\operatorname{H_0}:\beta_{r+1}=\cdots=\beta_q=0\),使用\(F\)检验
\[ F=\frac{(\operatorname{SSE}_r-\operatorname{SSE}/(q-r))}{\operatorname{SSE}/(n-q-1)}=\frac{\operatorname{MSR}}{\operatorname{MSE}} \]
在自由度为\(q-r\)和\(n-q-1\)的\(F\)分布中进行检验。
整体逻辑是看添加上其他自变量,是否显著增加拟合效果。如果\(\operatorname{H}_0\)为真,则可以化简模型,反之则不可以。
| 误差源 | 自由度(df) | 平方和 | 均方 | \(F\)值 |
|---|---|---|---|---|
| \(z_{t,r+1:q}\) | \(q-r\) | \(\operatorname{SSR}=\operatorname{SSE}_r-\operatorname{SSE}\) | \(\operatorname{MSR}=\operatorname{SSR}/(q-r)\) | \(F=\frac{\operatorname{MSR}}{\operatorname{MSE}}\) |
| Error | \(n-(q+1)\) | \(\operatorname{SSE}\) | \(\operatorname{MSE}=\operatorname{SSE}/(n-q-1)\) |
当\(\beta_1=\cdots=\beta_q=0\)时,\(x_t=\beta_0+w_t\),有:
\[ R^2=\frac{\operatorname{SSE}_0-\operatorname{SSE}}{\operatorname{SSE}_0}\\ \operatorname{SSE}_0=\sum_{t=1}^n(x_t-\bar x)^2 \]
\(R^2\)是决定系数(coefficient of determination)。
通过上述\(F\)检验来选择变量的纳入或删除,这就是逐步多元回归(stepwise multiple regression)。
下面介绍通过模型优度来进行模型选择的方法。
1.2.1 信息准则
\(k\)个系数的正态回归模型,方差的最大似然估计可表示为:
\[ \hat\sigma_k^2=\frac{\operatorname{SSE}(k)}{n} \]
其中\(\operatorname{SSE}(k)\)表示\(k\)个回归系数的模型的残差平方和。显然\(\operatorname{SSE}(k)\)会随着\(k\)的增加而单调减少。
信息准则的基本思路是在最小化\(\hat\sigma_k^2\)的同时,添加一个随\(k\)的增加而单调增加的惩罚项,来选择合适的参数数量。
1.2.1.1 Akaike信息准则(Akaike’s Information Criterion,AIC)
\[ \operatorname{AIC}=\log\hat\sigma_k^2+\frac{n+2k}{n} \tag{1}\]
最常用。
1.2.1.2 AIC,偏差修正(AICc)
\[ \operatorname{AICc}=\log\hat\sigma_k^2+\frac{n+k}{n-k-2} \]
适用于参数数量相对较大,但样本量较小的情况。
1.2.1.3 贝叶斯信息准则(Bayesian Information Criterion,BIC)
\[ \operatorname{BIC}=\log\hat\sigma_k^2+\frac{k\log n}{n} \]
BIC惩罚项的值远大于AIC,适合在大样本中选出较小的模型,防止过拟合。
这里的AIC,BIC都不是标准模式,是在正态分布线性回归中的一种等效形式。R中AIC()函数和BIC()函数使用的是通用形式。
以AIC为例,通用形式为:
\[ \operatorname{AIC}(k)=2k-2\log(L) \tag{2}\]
其中\(k\)是参数个数,\(L\)是似然函数最大值,这是AIC()函数得到的结果。在某些模型中可转换为:
\[ \operatorname{AIC}(k)=2k+n\log(\hat\sigma_k^2) \tag{3}\]
其中其中\(n\)是样本量,\(\hat\sigma_k^2\)是均方误差估计值。式 2和式 3在成立时是等价的,式 3可通过下列公式转换为式 1。
\[ \operatorname{AIC}_1=\frac{\operatorname{AIC}_2}{n}-\log(2\pi) \]
其中\(\operatorname{AIC}_1\)是式 1的值,\(\operatorname{AIC}_2\)是式 2的值。BIC也可以通过相似公式转换。
AIC和BIC的具体值并不是关注的重点,更需要关注的是一组模型中,同一算法下值的变化,值越小越好。
1.2.2 模型选择
图 2展示1970-1979年间洛杉矶温度、污染和心血管死亡率的变化。展现出强烈的对于冬夏季节的变化,且死亡率整体为下降趋势。
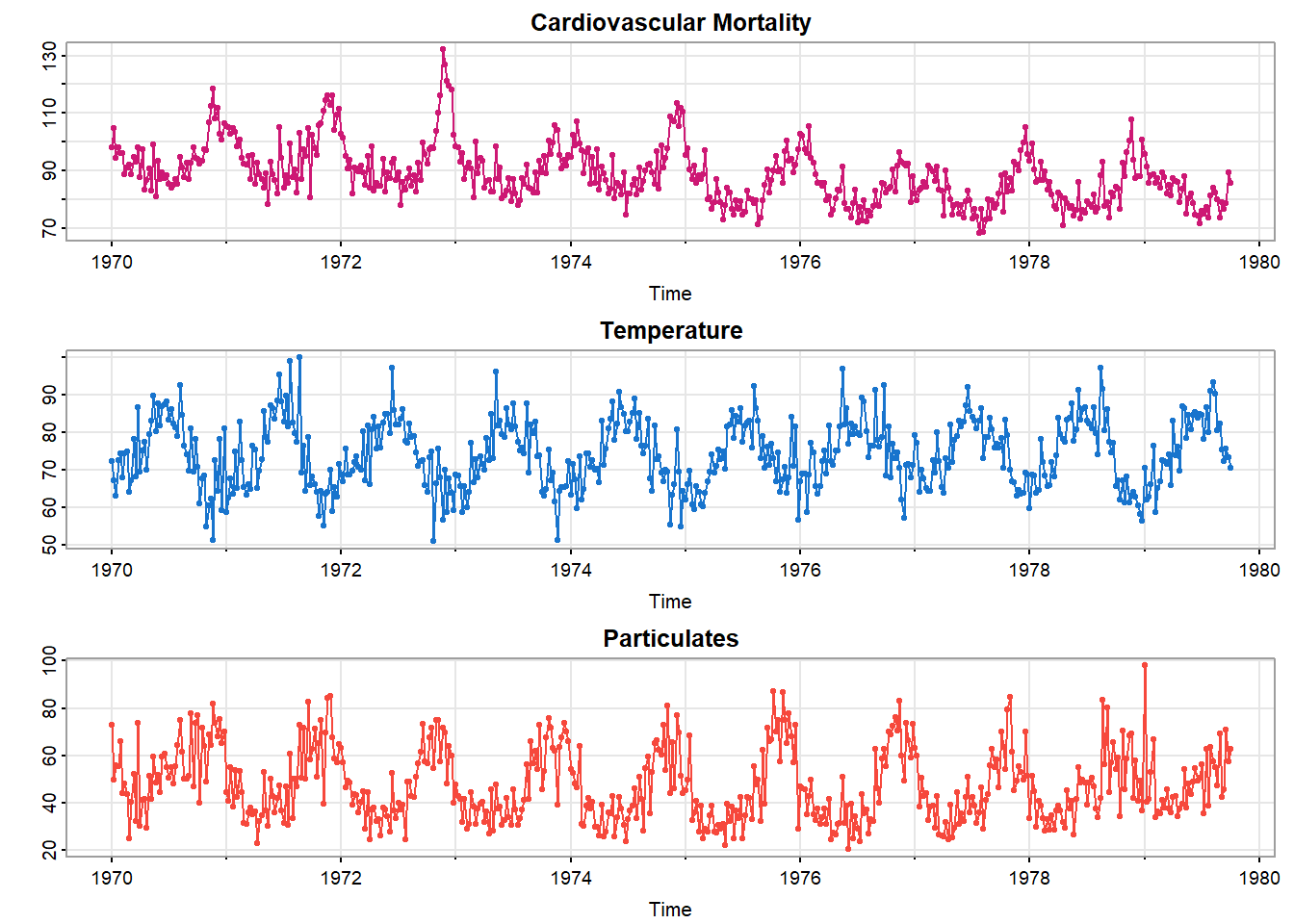
我们可以假设\(4\)种模型,其中\(M_t\)表示心血管死亡率,\(T_t\)表示温度,\(P_t\)表示颗粒水平,\(T.\)是\(T_t\)的平均值\(74.26\),用于调整温度,避免共线性问题。模型如下:
\[ M_t=\beta_0+\beta_1t+w_t \tag{4}\] \[ M_t=\beta_0+\beta_1t+\beta_2(T_t-T.)+w_t \tag{5}\] \[ M_t=\beta_0+\beta_1t+\beta_2(T_t-T.)+\beta_3(T_t-T.)^2+w_t \tag{6}\] \[ M_t=\beta_0+\beta_1t+\beta_2(T_t-T.)+\beta_3(T_t-T.)^2+\beta_4P_t+w_t \tag{7}\]
式 4是简单的趋势模型;式 5额外添加了线性的温度变量;式 6温度变量是二次的;式 7还添加了污染变量。
对比式 4和式 7,检验\(\operatorname{H}_0:\beta_2=\beta_3=\beta_4=0\)。
\[ F_{3,503}=\frac{(40020-20508)/3}{20508/503}\approx160>F_{3,503}(0.001) \]
拒绝\(\operatorname{H}_0\)。
temp = tempr - mean(tempr)
temp2 = temp ^ 2
trend = time(cmort)
fit = lm(cmort ~ trend + temp + temp2 + part, na.action = NULL) # na.action用来保存残差和拟合值的时间属性
summary(fit)
Call:
lm(formula = cmort ~ trend + temp + temp2 + part, na.action = NULL)
Residuals:
Min 1Q Median 3Q Max
-19.0760 -4.2153 -0.4878 3.7435 29.2448
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2831.490246 199.556899 14.19 < 2e-16 ***
trend -1.395901 0.101009 -13.82 < 2e-16 ***
temp -0.472469 0.031622 -14.94 < 2e-16 ***
temp2 0.022588 0.002827 7.99 9.26e-15 ***
part 0.255350 0.018857 13.54 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.385 on 503 degrees of freedom
Multiple R-squared: 0.5954, Adjusted R-squared: 0.5922
F-statistic: 185 on 4 and 503 DF, p-value: < 2.2e-16进一步分析就需要检查残差\(\hat w_t=M_t-\hat M_t\)的自相关,这个在第三章会进行讲解。
1.2.3 滞后回归(Lagged Regression)
ccf2(soi, rec, main="SOI vs 新鱼数量")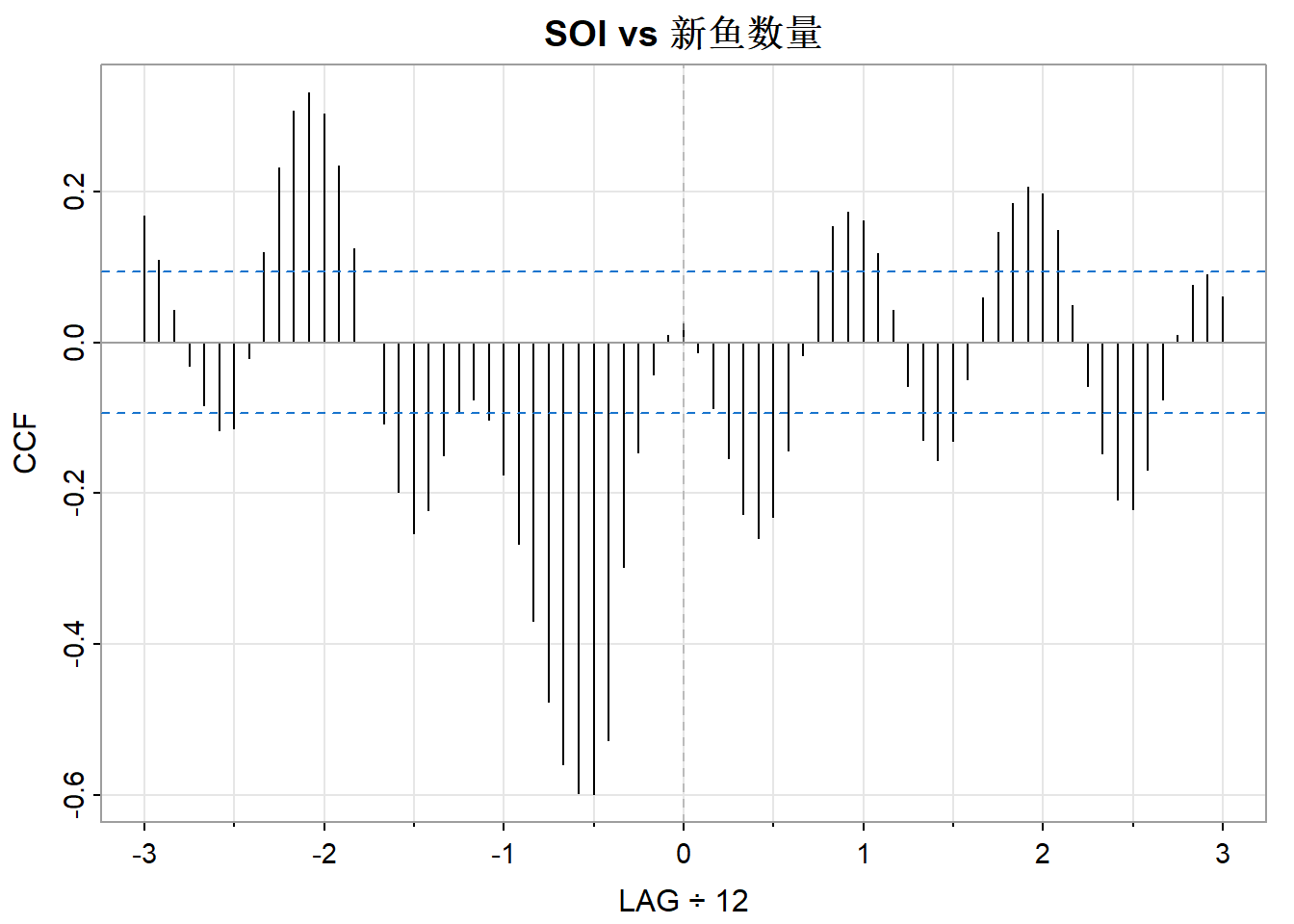
图 4是第一章中提到的SOI和新鱼数量数据,当时是认为时间\(t-6\)测量的SOI和时间\(t\)的新鱼数量相关,现在进行检验(虽然这不是线性的,但我们先用线性进行检验)。
模型如下:
\[ R_t=\beta_0+\beta_1S_{t-6}+w_t \]
其中\(R_t\)是时间\(t\)时的新鱼数量,\(S_{t-6}\)是时间\(t-6\)时的SOI,假设\(w_t\)是白噪声。
# 创建对齐的数据框
fish = ts.intersect(rec, soiL6 = stats::lag(soi, -6), dframe = TRUE)
summary(fit <- lm(rec ~ soiL6, data = fish, na.action = NULL))
Call:
lm(formula = rec ~ soiL6, data = fish, na.action = NULL)
Residuals:
Min 1Q Median 3Q Max
-65.187 -18.234 0.354 16.580 55.790
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 65.790 1.088 60.47 <2e-16 ***
soiL6 -44.283 2.781 -15.92 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 22.5 on 445 degrees of freedom
Multiple R-squared: 0.3629, Adjusted R-squared: 0.3615
F-statistic: 253.5 on 1 and 445 DF, p-value: < 2.2e-16也可以借助dynlm包来完成。
library(dynlm)
summary(fit2 <- dynlm(rec ~ L(soi, 6)))
Time series regression with "ts" data:
Start = 1950(7), End = 1987(9)
Call:
dynlm(formula = rec ~ L(soi, 6))
Residuals:
Min 1Q Median 3Q Max
-65.187 -18.234 0.354 16.580 55.790
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 65.790 1.088 60.47 <2e-16 ***
L(soi, 6) -44.283 2.781 -15.92 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 22.5 on 445 degrees of freedom
Multiple R-squared: 0.3629, Adjusted R-squared: 0.3615
F-statistic: 253.5 on 1 and 445 DF, p-value: < 2.2e-16fit2还保留了时间信息。
par(mfrow=2:1)
tsplot(resid(fit))
acf1(resid(fit))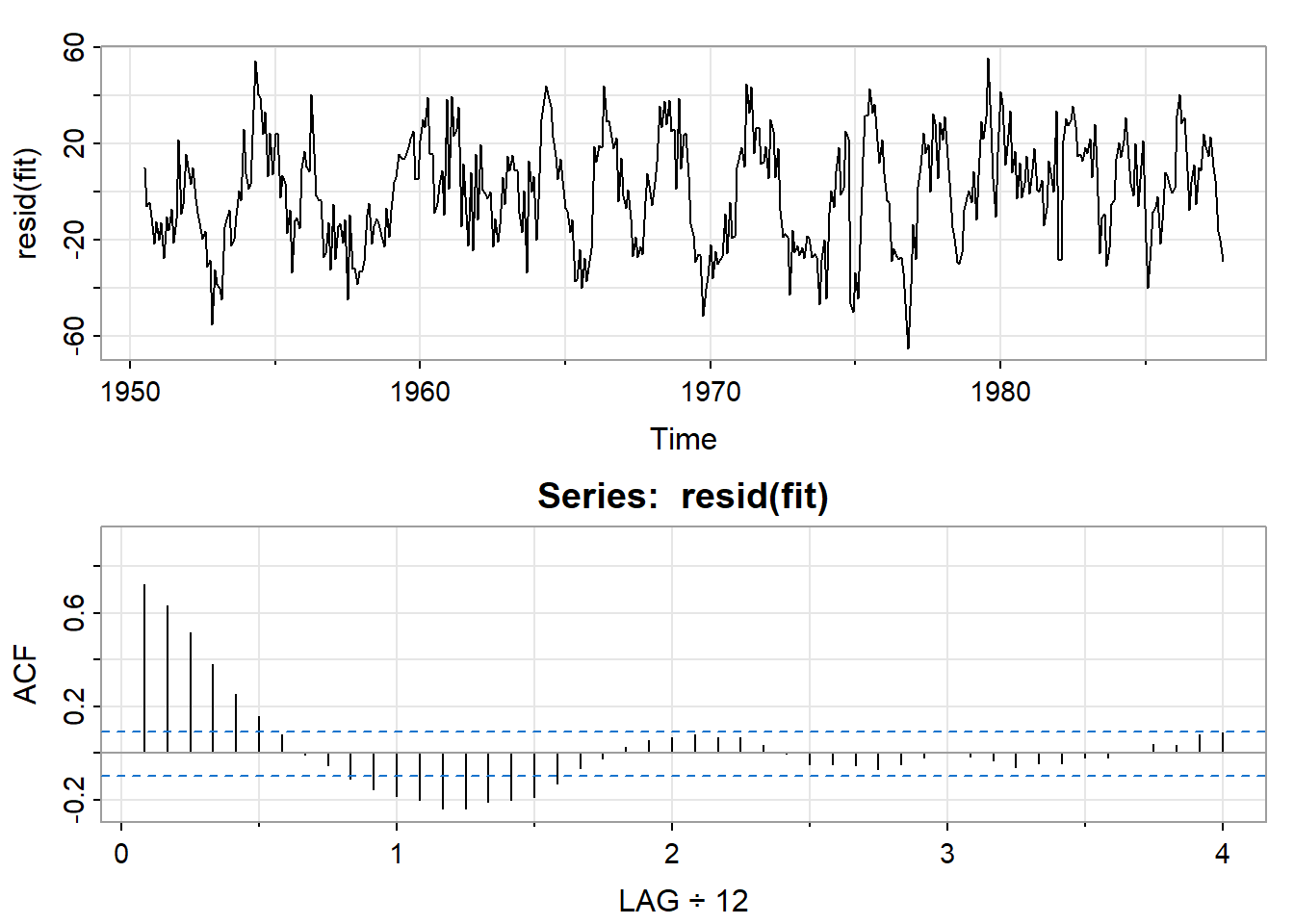
可见残差不是白噪声,后续会讲解进一步的分析。
2 探索性数据分析
之前讲述的分析方法都有一个前提假设:时间序列数据是平稳的。但现实中的数据很多都不能满足这个前提假设,本节会提及一些方法来淡化非平稳性的影响。
最简单的非平稳模型可能是趋势平稳(trend stationary)模型,其过程具有围绕趋势的平稳性,模型如下:
\[ x_t=\mu_t+y_t \]
其中\(x_t\)是观测值,\(\mu_t\)是趋势,\(y_t\)是平稳过程。\(\mu_t\)会模糊掉\(y_t\),因此经常会考虑消除掉\(\hat\mu_t\),使用残差分析。
\[ \hat y_t=x_t-\hat\mu_t \]
2.1 去趋势(Detrended)和差分(Difference)
图 1中模型形式为:
\[ x_t=\mu_t+y_t \tag{8}\]
去除线性趋势:
\[ \mu_t=\beta_0+\beta_1t \tag{9}\]
最小二乘法估计得到:
\[ \hat\mu_t=-3.59t+7131 \]
得到:
\[ \hat y_t=x_t-3.59t+7131 \]
par(mfrow = 2:1)
tsplot(detrend(chicken), main = "去趋势")
tsplot(diff(chicken), main = "差分")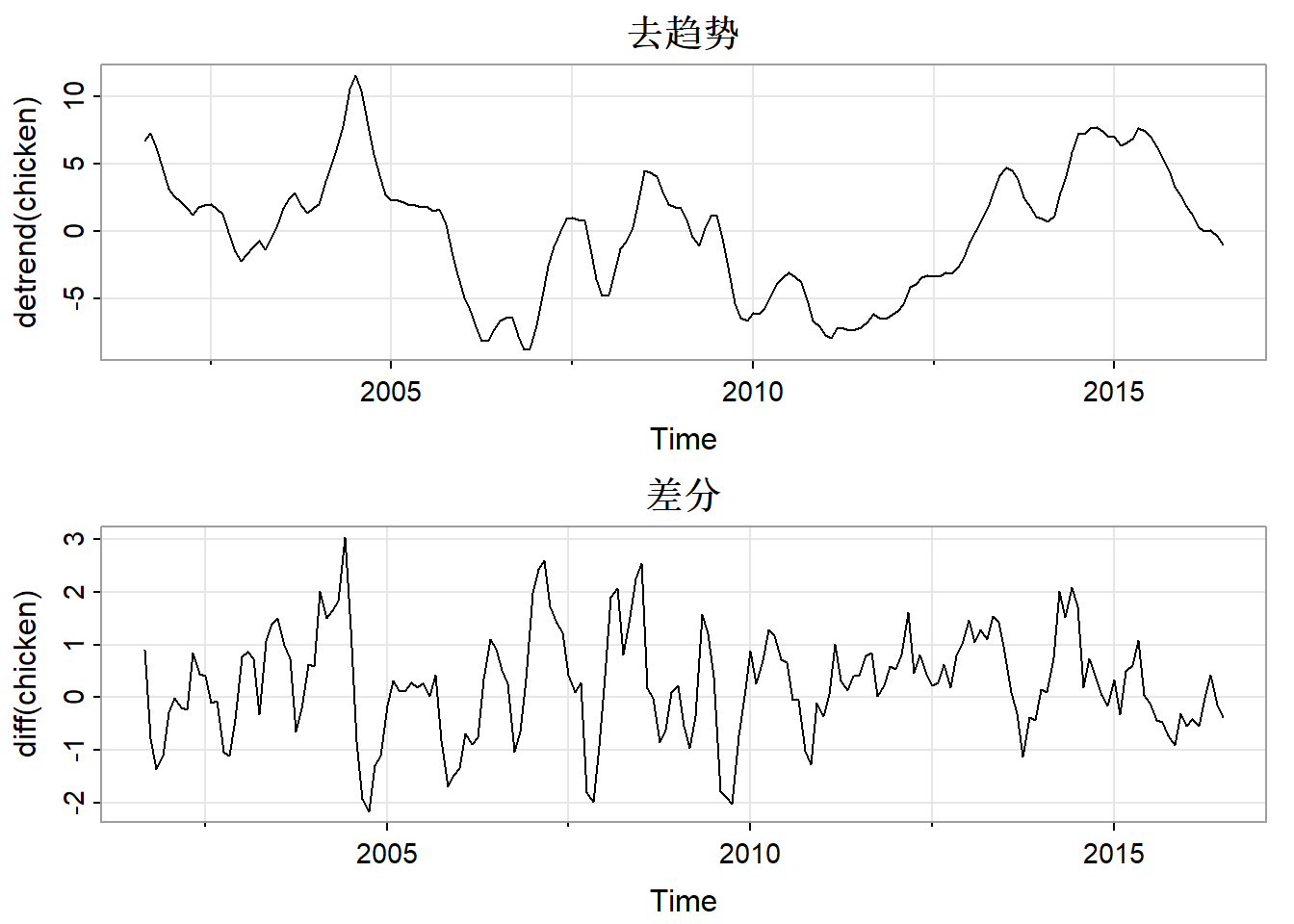
par(mfrow = c(3, 1))
acf1(chicken, 48, main = "原始")
acf1(detrend(chicken), 48, main = "去趋势")
acf1(diff(chicken), 48, main = "差分")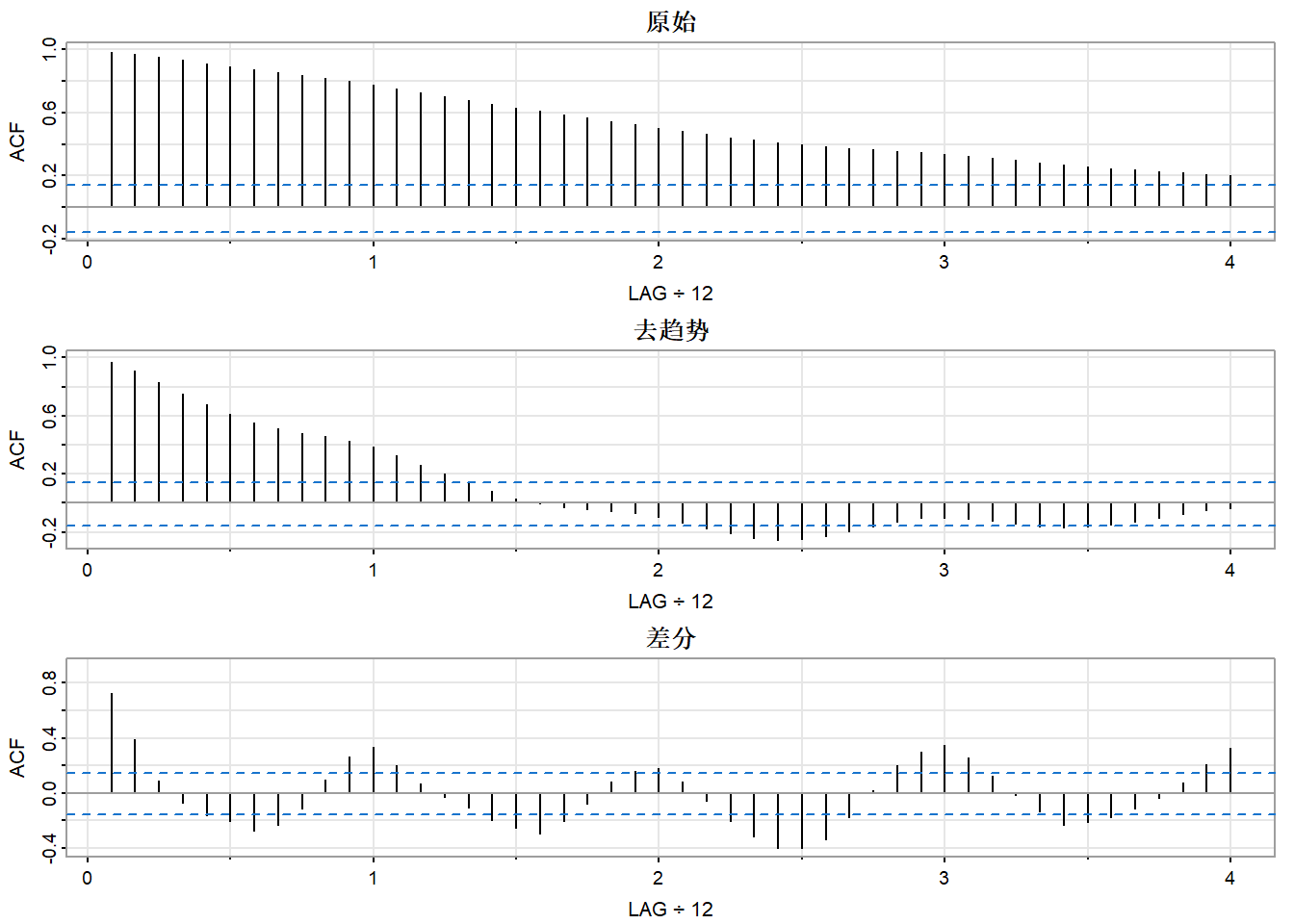
在这里差分可能是一种更好的办法。去趋势是把趋势固定来建模(如式 9),差分是用带漂移项的随机游走模型来表示趋势模型:
\[ \mu_t=\delta+\mu_{t-1}+w_t \]
其中\(w_t\)是与\(y_t\)无关的白噪声。
针对式 8进行差分,有:
\[ x_t-x_{t-1}=(\mu_t+y_t)-(\mu_{t-1}+y_{t-1})=\delta+w_t+y_t-y_{t-1} \]
\(x_t-x_{t-1}\)是平稳的。
差分消除趋势的优点是不需要估计参数,缺点是破坏了\(y_t\)的结构。
一阶差分可以表示为:
\[ \nabla x_t=x_t-x_{t-1} \tag{10}\]
式 10的差分就是二阶差分,以此类推。
2.1.1 后移算子(Backshift Operator)
后移算子用来表示高阶差分。
定义后移算子为:
\[ Bx_t=x_{t-1} \]
可以扩展为\(B^2x_t=B(Bx_t)=Bx_{t-1}=x_{t-2}\),以此类推:
\[ B^kx_t=x_{t-k} \]
要求\(B^{-1}B=1\),给出逆算子的概念:
\[ x_t=B^{-1}Bx_t=B^{-1}x_{t-1} \]
\(B^{-1}\)是前移算子(Forward-shift Operator)。
式 10可以写为:
\[ \nabla x_t=(1-B)x_t \]
二阶差分为:
\[ \nabla^2x_t=(1-B)^2x_t=(1-2B+B^2)x_t=x_t-2x_{t-1}+x_{t-2} \]
2.1.2 \(d\)阶差分(Differences of order \(d\))
\[ \nabla^d=(1-B)^d \tag{11}\]
当\(d=1\)时可以省略。
2.1.3 全球温度数据的差分
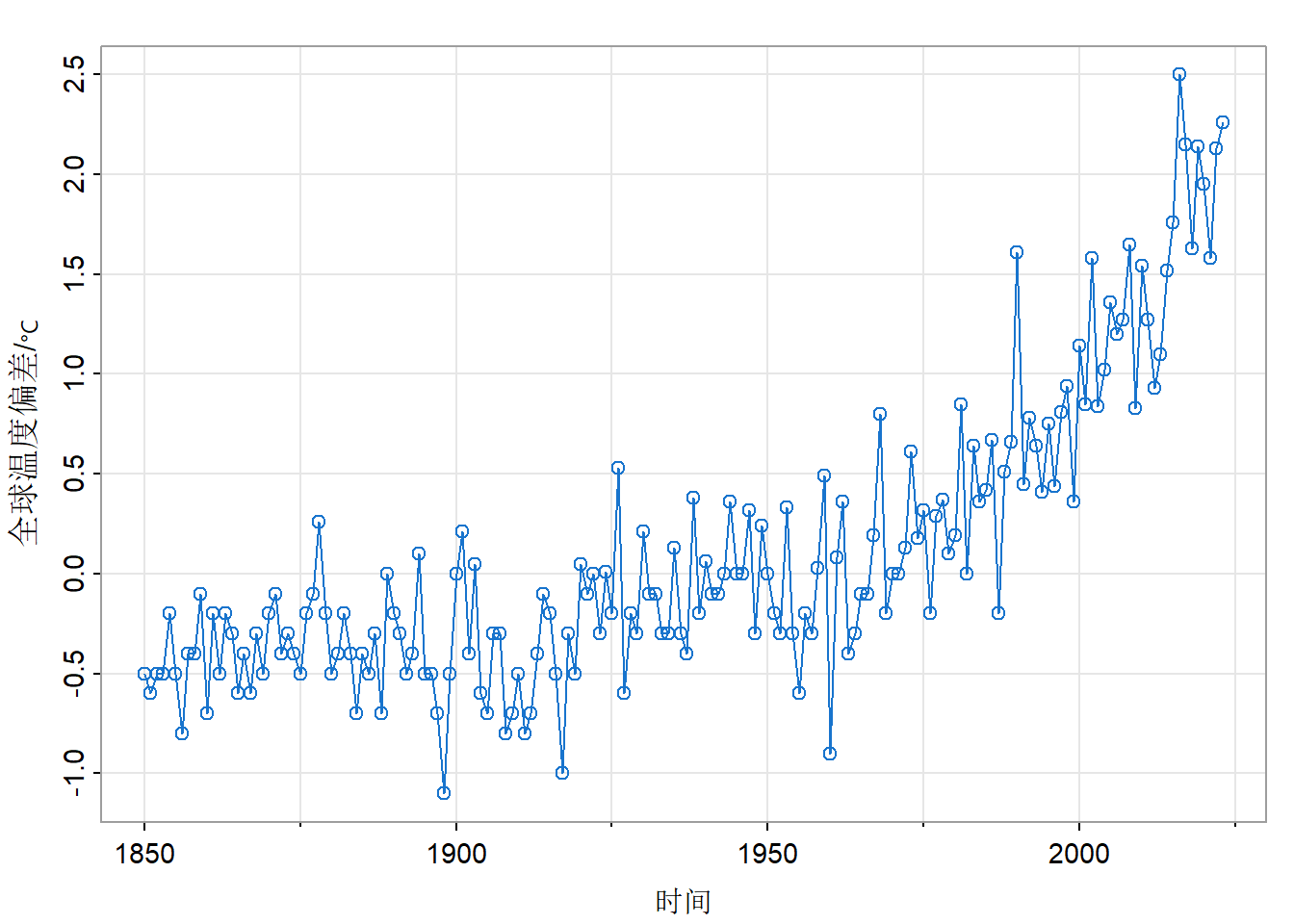
par(mfrow = c(2, 1))
tsplot(diff(gtemp_land), type = "o")
acf1(diff(gtemp_land), 48, main = "")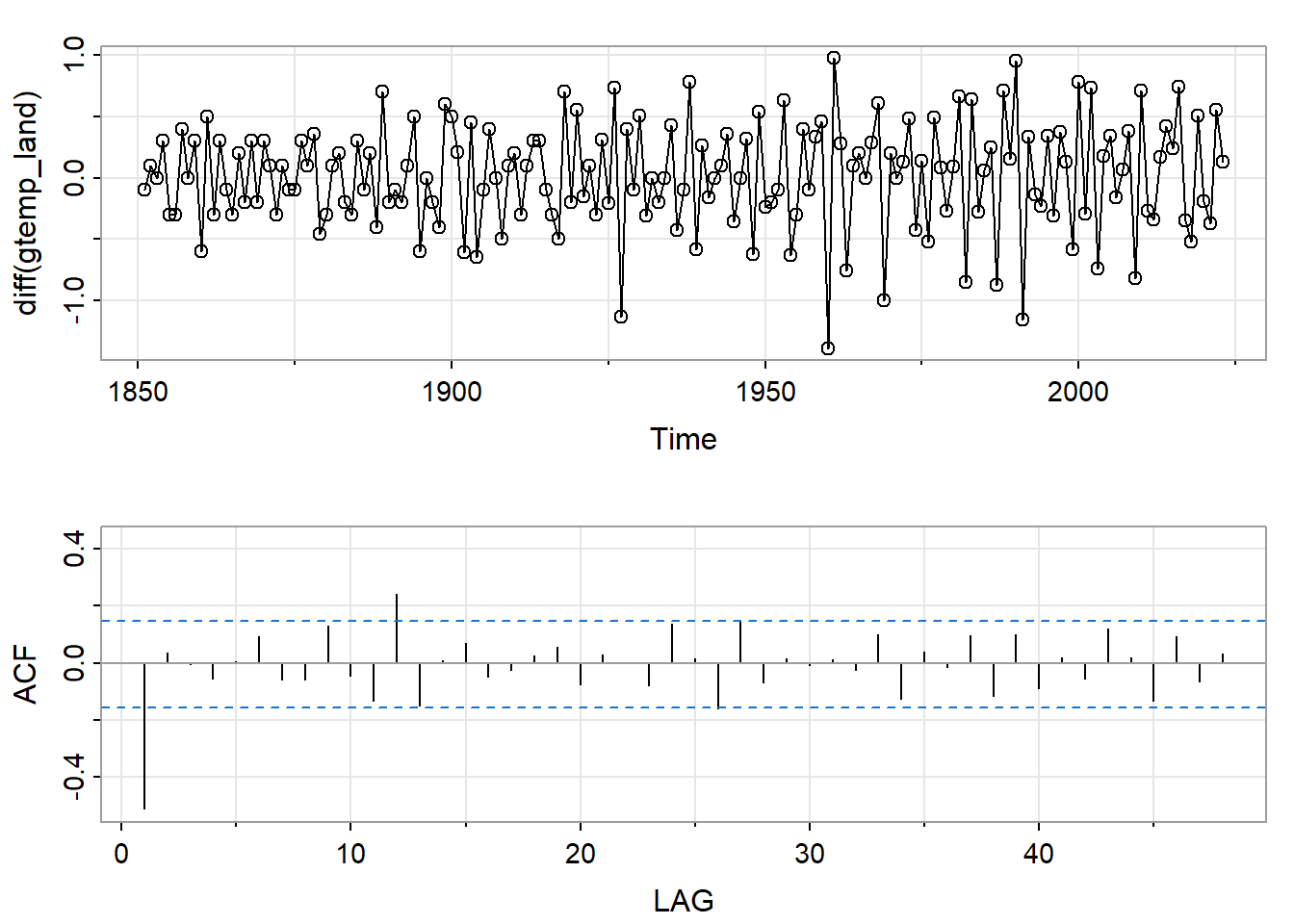
差分后自相关很小,说明该序列几乎是带漂移项的随机游走。使用mean(diff(gtemp_land))计算得到差分平均值约为0.016,说明每100年增加1.6摄氏度。
2.1.4 分数差分(Fractional Differencing)和变换
分数差分就是把差分算子(式 11)扩展到分数幂\(-0.5<d<0.5\),常见于长记忆时间序列,会在第五章进行详细讨论。
有时对数据进行变换可能更有助于我们分析,常见的变换有:
\[ y_t=\log x_t \]
和
\[ y_t=\begin{cases} (x^{\lambda}_t-1)/\lambda&\lambda\neq0\\ \log x_t&\lambda=0 \end{cases} \]
前一种适合原始序列数值较大且波动较大的情况,后一种是Box-Cox的幂律变换(power transformations),细节详见 Shumway & Stoffer (1992) 文献的4.7节。
这些变换也用于提高和正态性的相似性以及增强两个序列之间的线性关系。
2.1.5 古气候冰川纹层
春季的时候冰川就会发生融化,会因为沙子、淤泥沉积形成的纹层(varve),这些纹层可以用来反映古气候参数。图 10 的上图展示了马萨诸塞州某地纹层情况,下图是对数变换后的数据。
layout(matrix(1:4,2), widths=c(2.5,1))
tsplot(varve, main="", ylab="", col=4)
mtext("varve", side=3, line=.5, cex=1.2, font=2, adj=0)
tsplot(log(varve), main="", ylab="", col=4)
mtext("log(varve)", side=3, line=.5, cex=1.2, font=2, adj=0)
qqnorm(varve, main="", col=4)
qqline(varve, col=2, lwd=2)
qqnorm(log(varve), main="", col=4)
qqline(log(varve), col=2, lwd=2)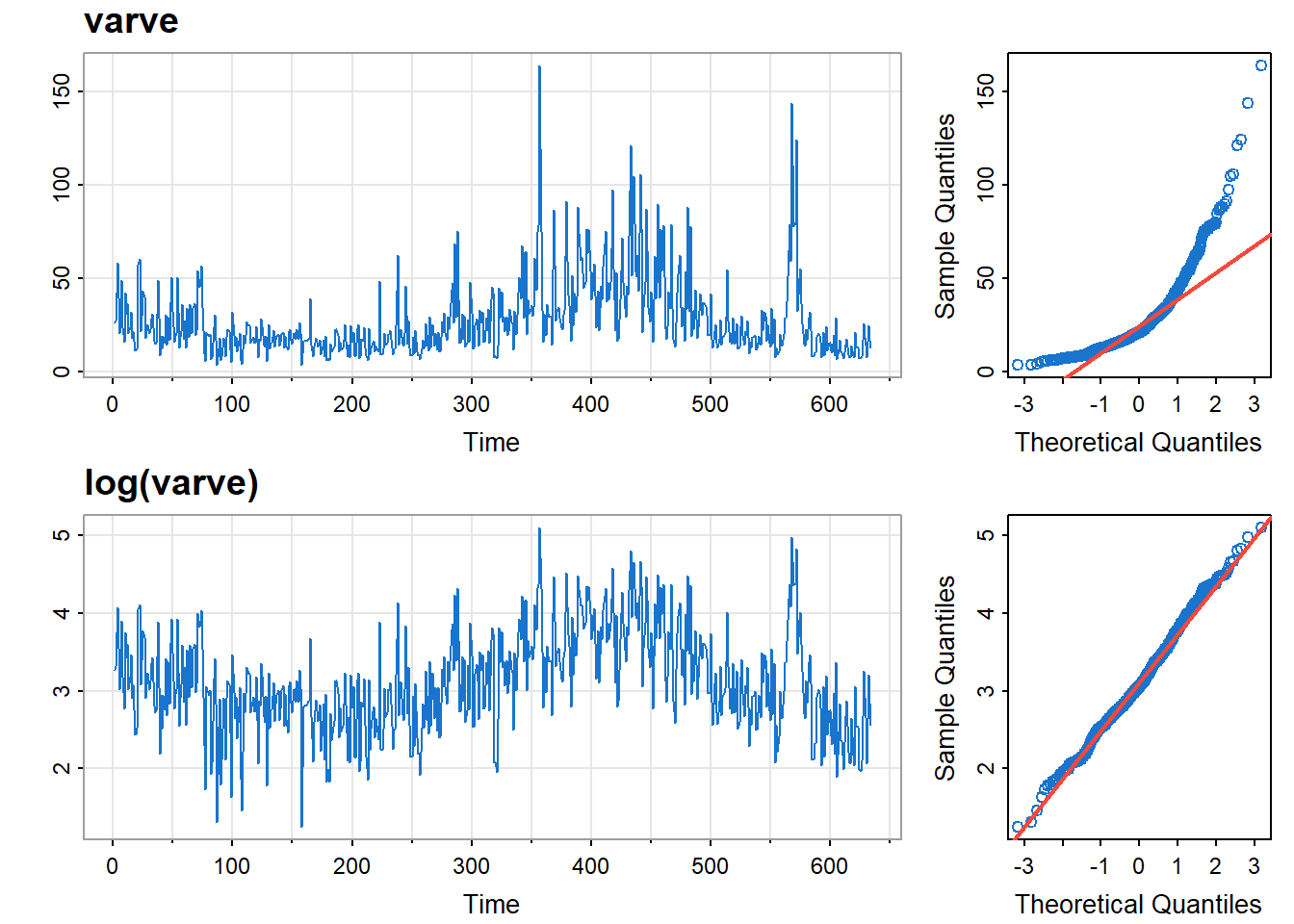
可见对数变换后正态性得到改善。
plot(log(varve))
acf(log(varve))
plot(log(varve))
acf(log(varve))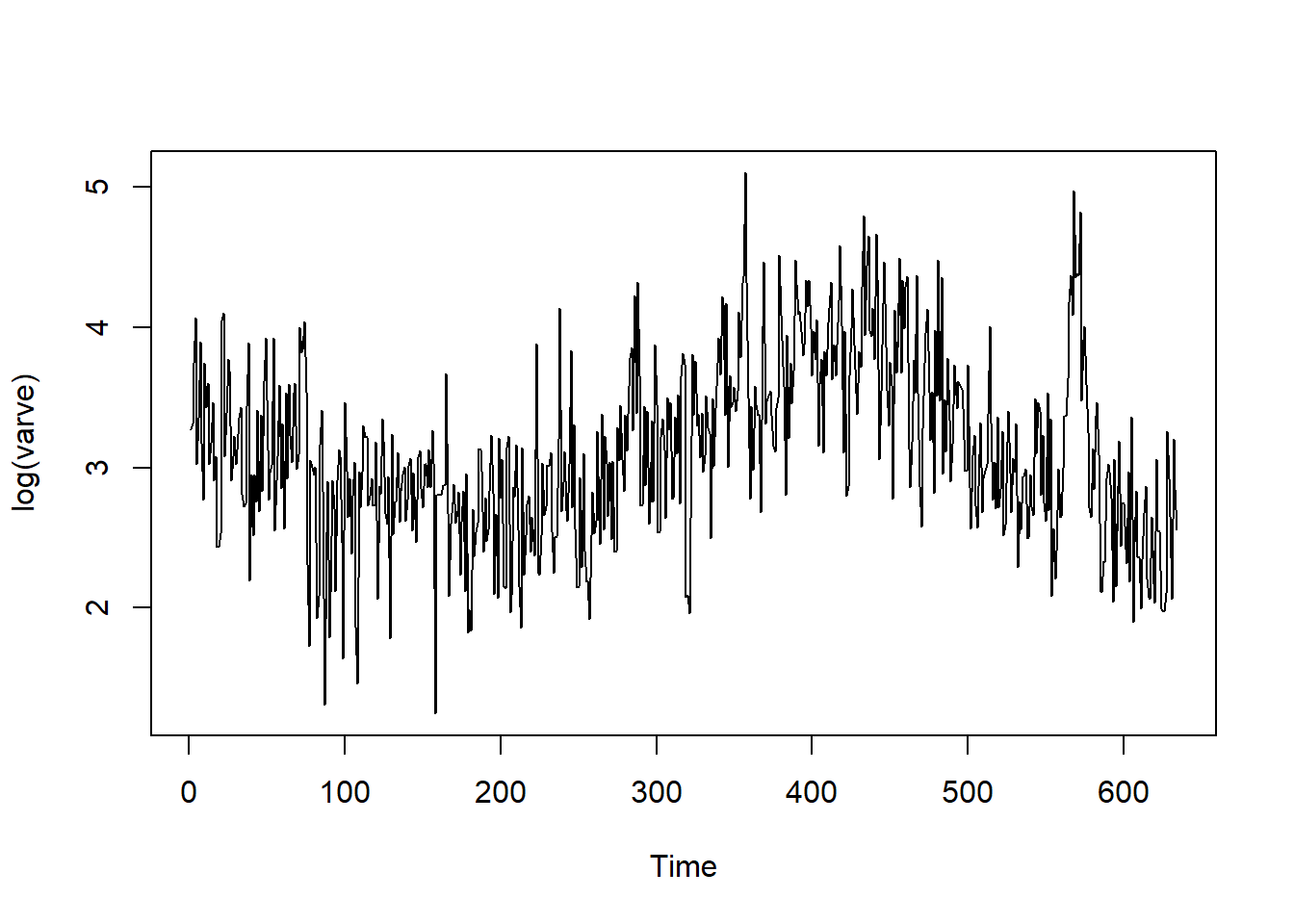
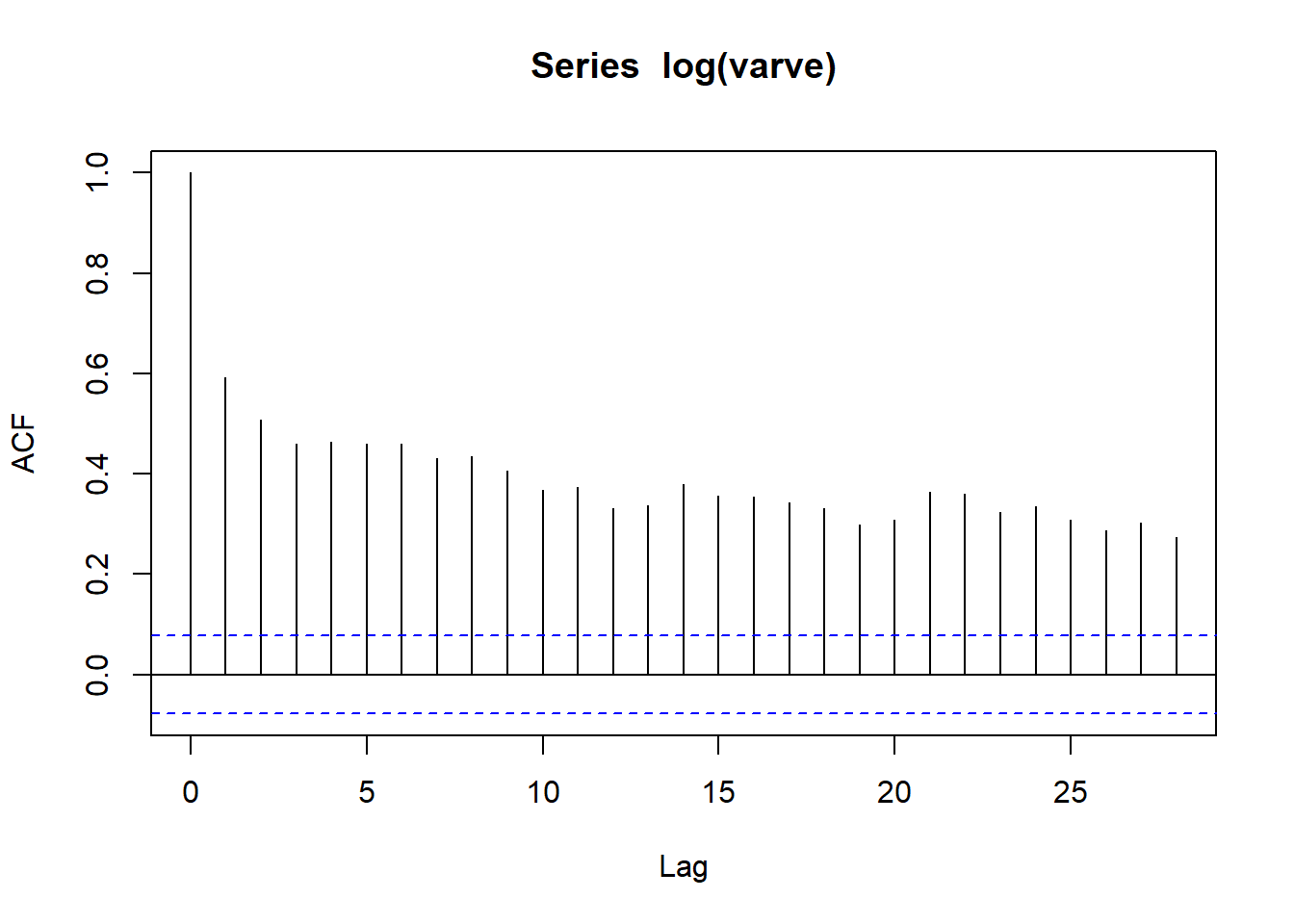
可见一阶差分后在滞后\(h=1\)时显著负相关。
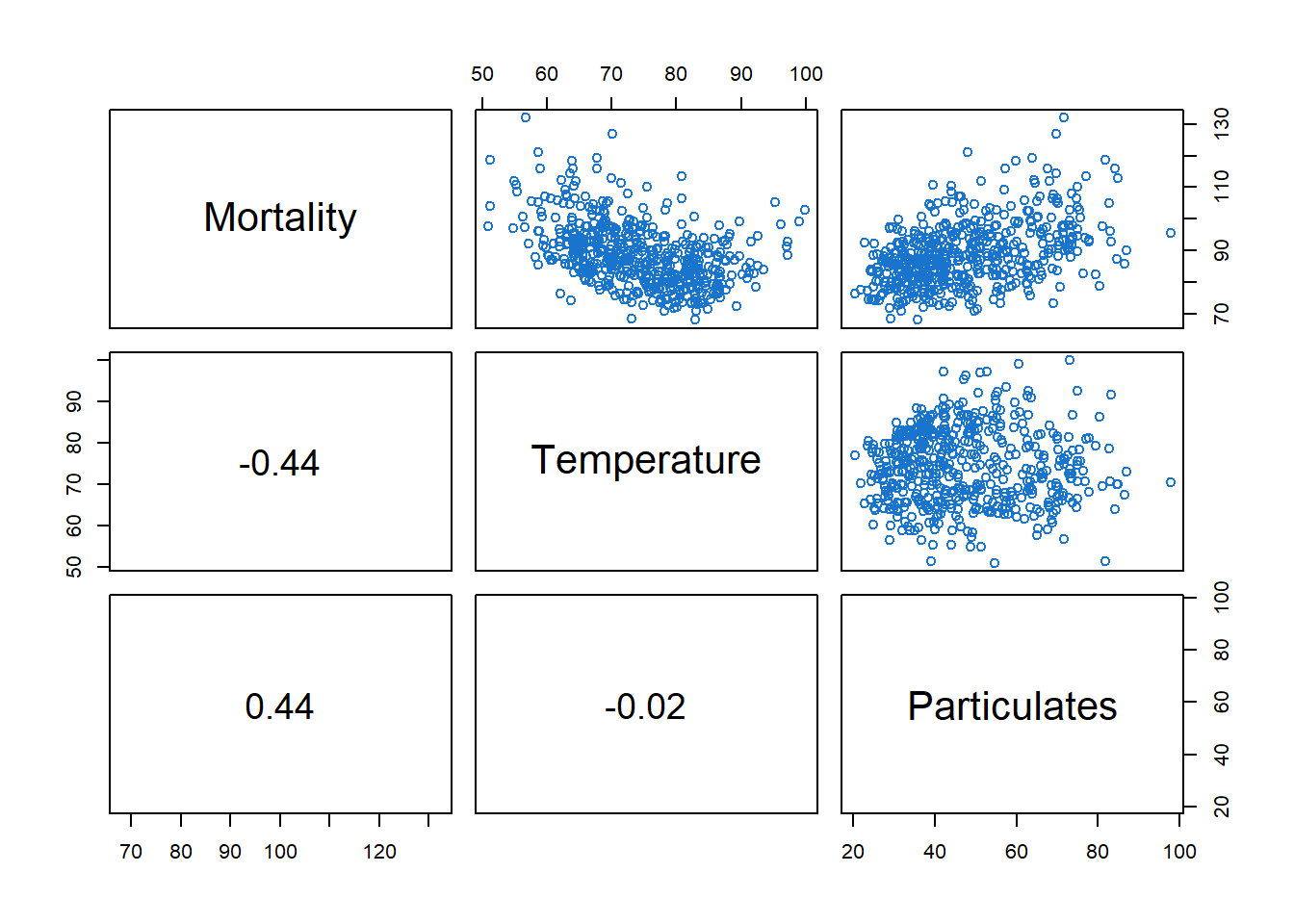
2.2 散点图矩阵
散点图矩阵可以帮助我们观察数据的相关性和是否是线性关系。图 13展示了SOI在\(t\)(\(S_t\))和\(t-h\)(\(S_{t-h}\))时的相关性,右上角是相关系数,红线是局部加权的散点图平滑(Locally Weighted Scatterplot Smoothing,lowess)。
lag1.plot(soi, 12, col=astsa.col(4, .3), cex=1.5, pch=20)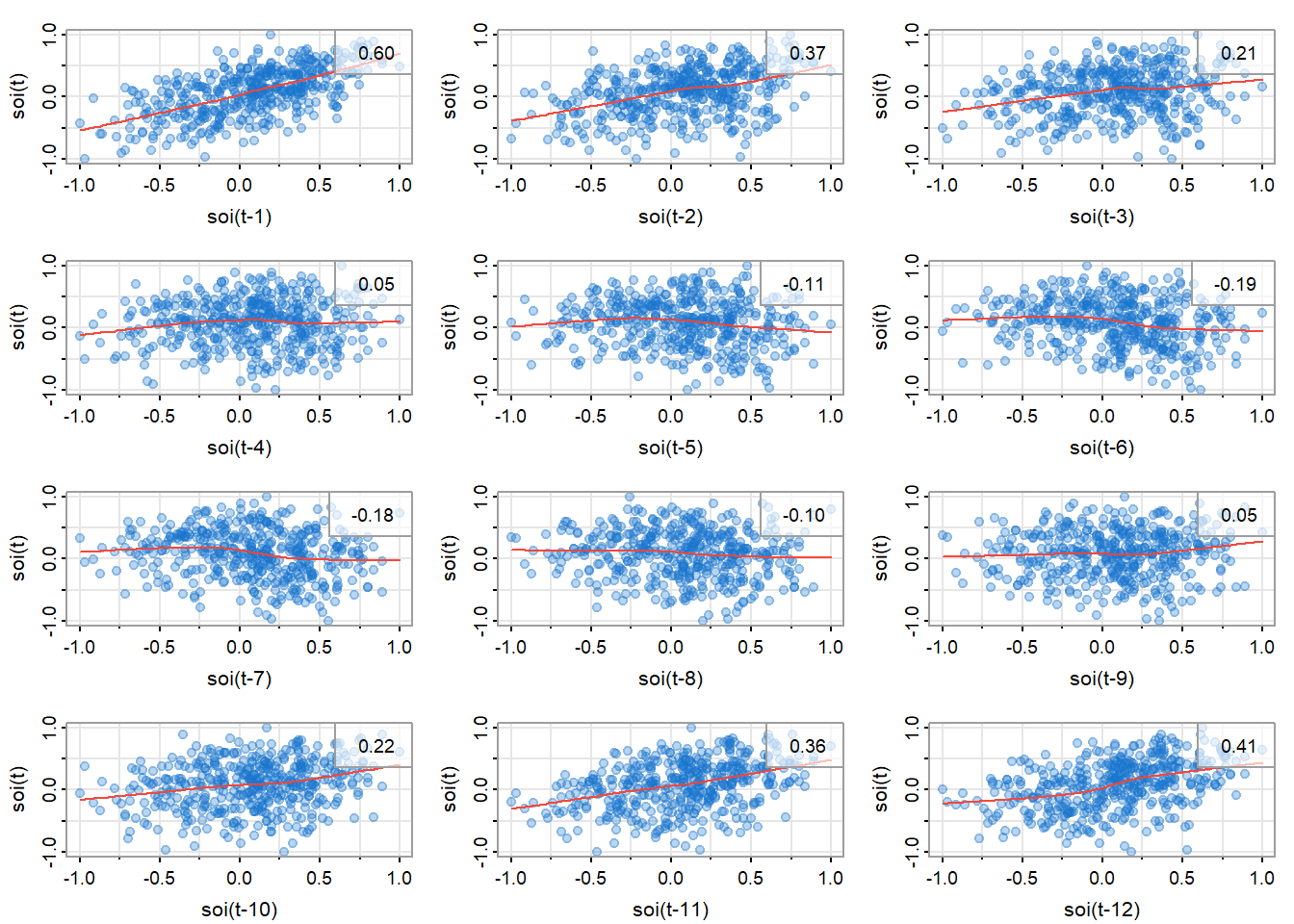
可以观察到,在滞后\(h=1,\ 2,\ 11,\ 12\)处强相关,这和图 14里观察到的一致。
acf1(soi, main="SOI")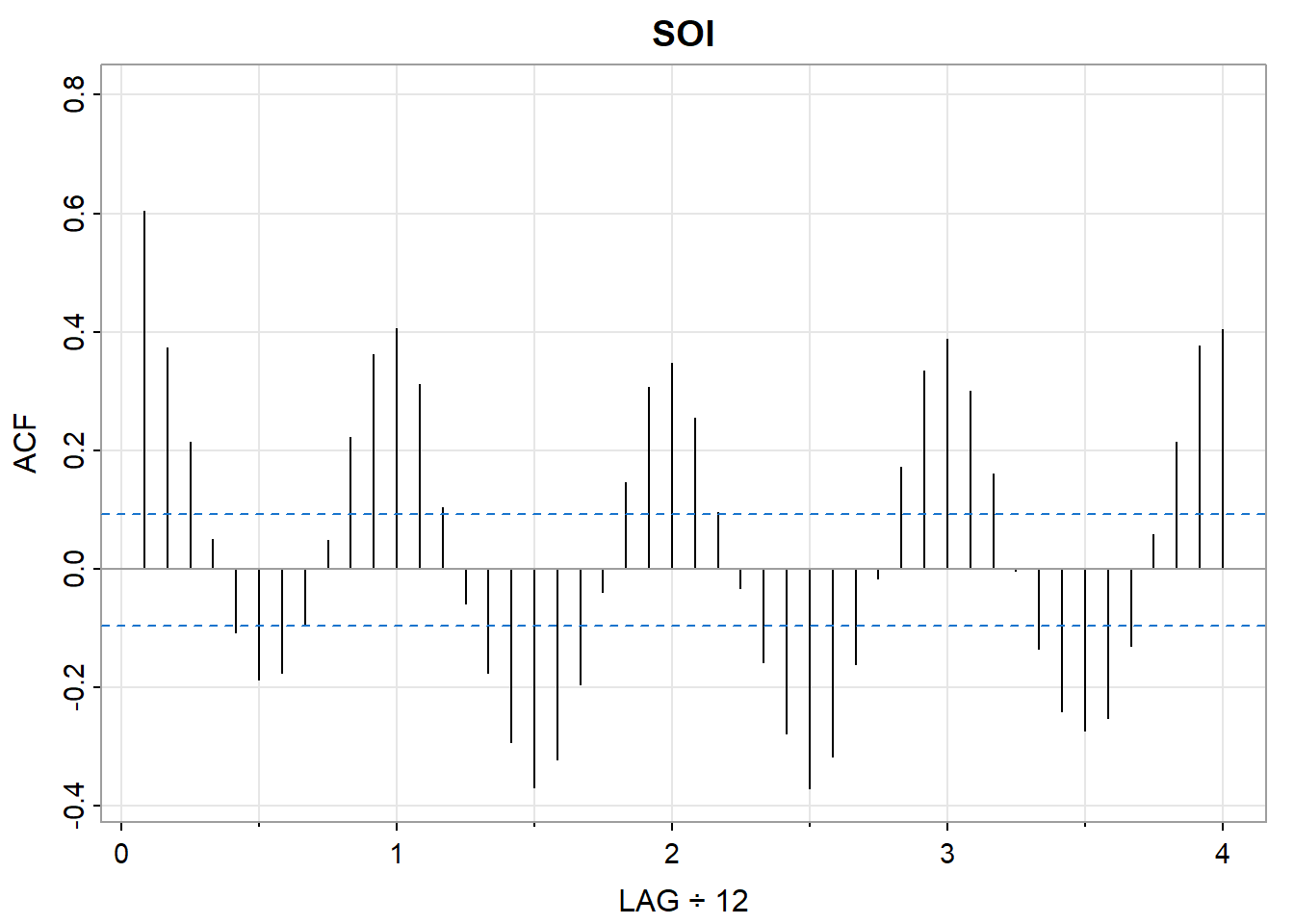
图 15展示了新鱼数量系列\(t\)时(\(R_t\))和\(S_{t-h}\)的相关性。
lag2.plot(soi, rec, 8, col=astsa.col(4, .3), cex=1.5, pch=20)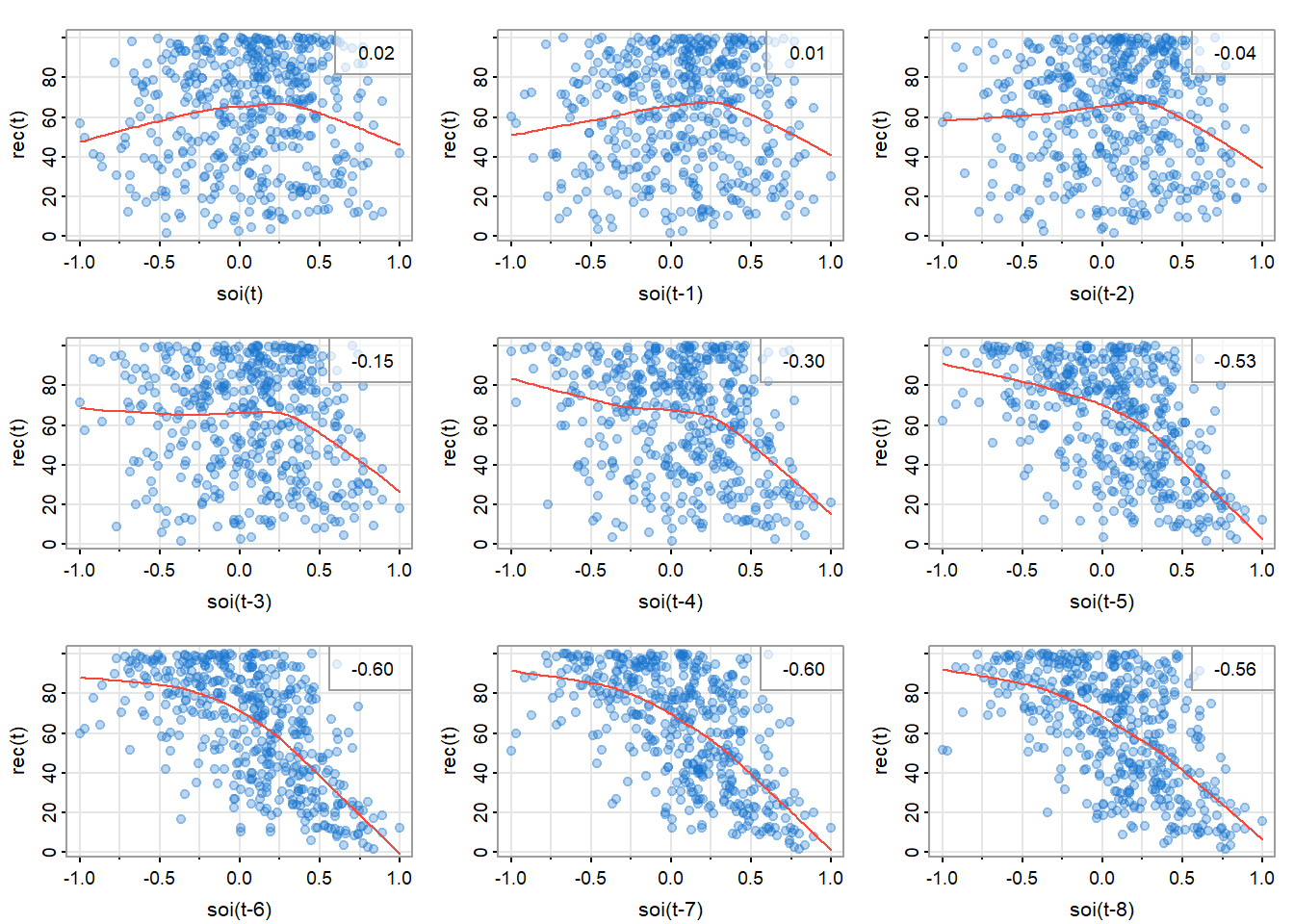
可以观察到是非线性相关,且SOI正值和负值与新鱼数量的关系不一样。
2.3 滞后回归(续)
在小节 1.2.3中,我们将新鱼数量序列对滞后SOI进行回归:
\[ R_t=\beta_0+\beta_1S_{t-6}+w_t \]
但图 15显示其不是线性关系,通过添加虚拟变量来表示非线性关系。
\[ R_t=\beta_0+\beta_1S_{t-6}+\beta_2D_{t-6}+\beta_3D_{t-6}S_{t-6}+w_t \]
其中\(D_t\)是虚拟变量,如果\(S_t<0\)则为0,否则为1。也可以写为:
\[ R_t=\begin{cases} \beta_0+\beta_1S_{t-6}+w_t&S_{t-6}<0\\ (\beta_0+\beta_2)+(\beta_1+\beta_3)S_{t-6}+w_t&S_{t-6}\ge0 \end{cases} \]
dummy = ifelse(soi < 0, 0, 1)
fish = ts.intersect(
rec,
soiL6 = stats::lag(soi, -6),
dL6 = stats::lag(dummy, -6),
dframe = TRUE
)
summary(fit <- lm(rec ~ soiL6 * dL6, data = fish, na.action = NULL))
Call:
lm(formula = rec ~ soiL6 * dL6, data = fish, na.action = NULL)
Residuals:
Min 1Q Median 3Q Max
-63.291 -15.821 2.224 15.791 61.788
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 74.479 2.865 25.998 < 2e-16 ***
soiL6 -15.358 7.401 -2.075 0.0386 *
dL6 -1.139 3.711 -0.307 0.7590
soiL6:dL6 -51.244 9.523 -5.381 0.00000012 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 21.84 on 443 degrees of freedom
Multiple R-squared: 0.4024, Adjusted R-squared: 0.3984
F-statistic: 99.43 on 3 and 443 DF, p-value: < 2.2e-16tsplot(
fish$soiL6,
fish$rec,
type = 'p',
col = 4,
ylab = 'rec',
xlab = 'soiL6'
)
lines(lowess(fish$soiL6, fish$rec), col = 4, lwd = 2)
points(fish$soiL6, fitted(fit), pch = '+', col = 6)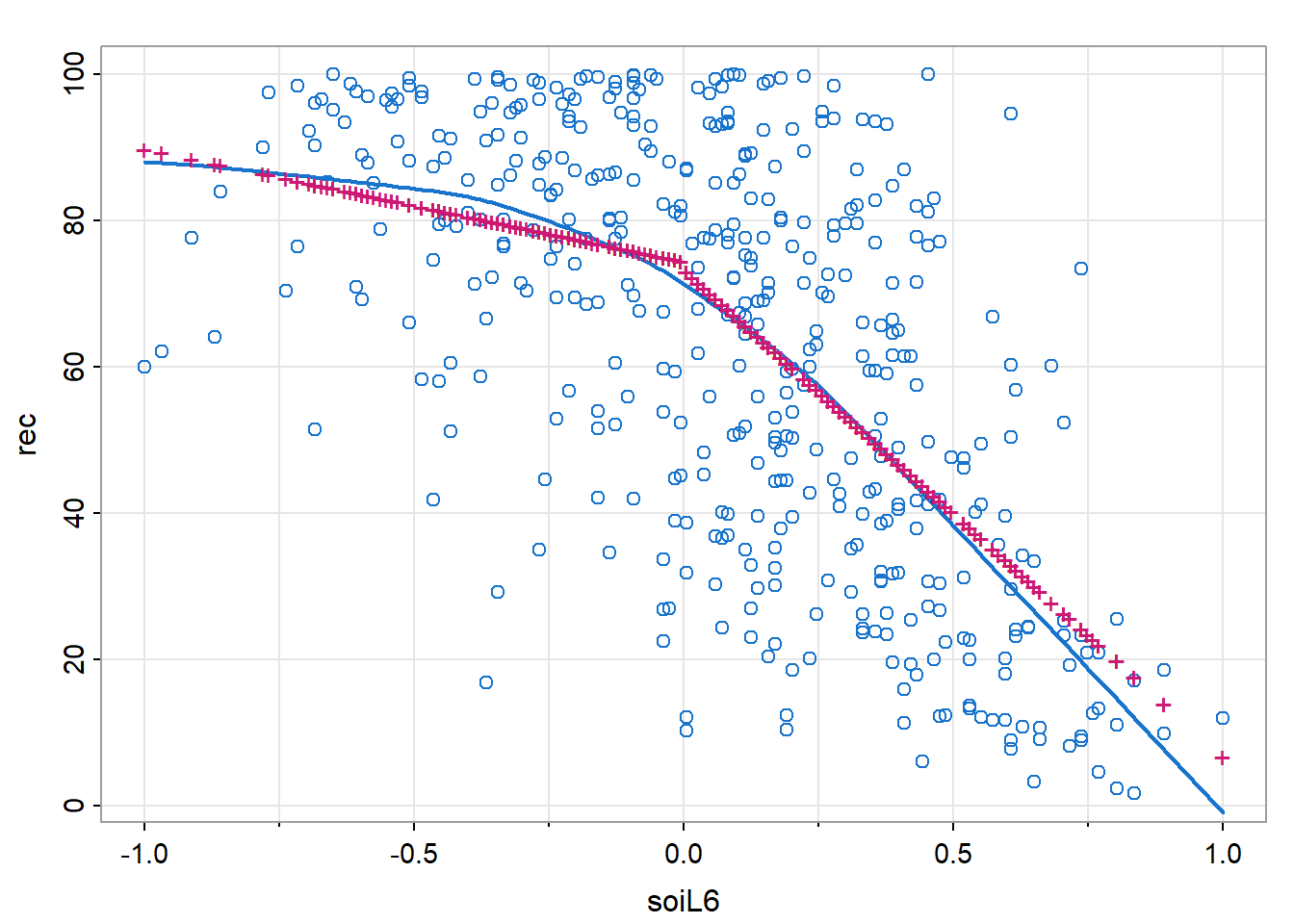
图 16中“+”是回归的拟合值,直线是lowess的拟合值。
图 17对回归拟合后的残差进行了探索。
tsplot(resid(fit))
acf1(resid(fit))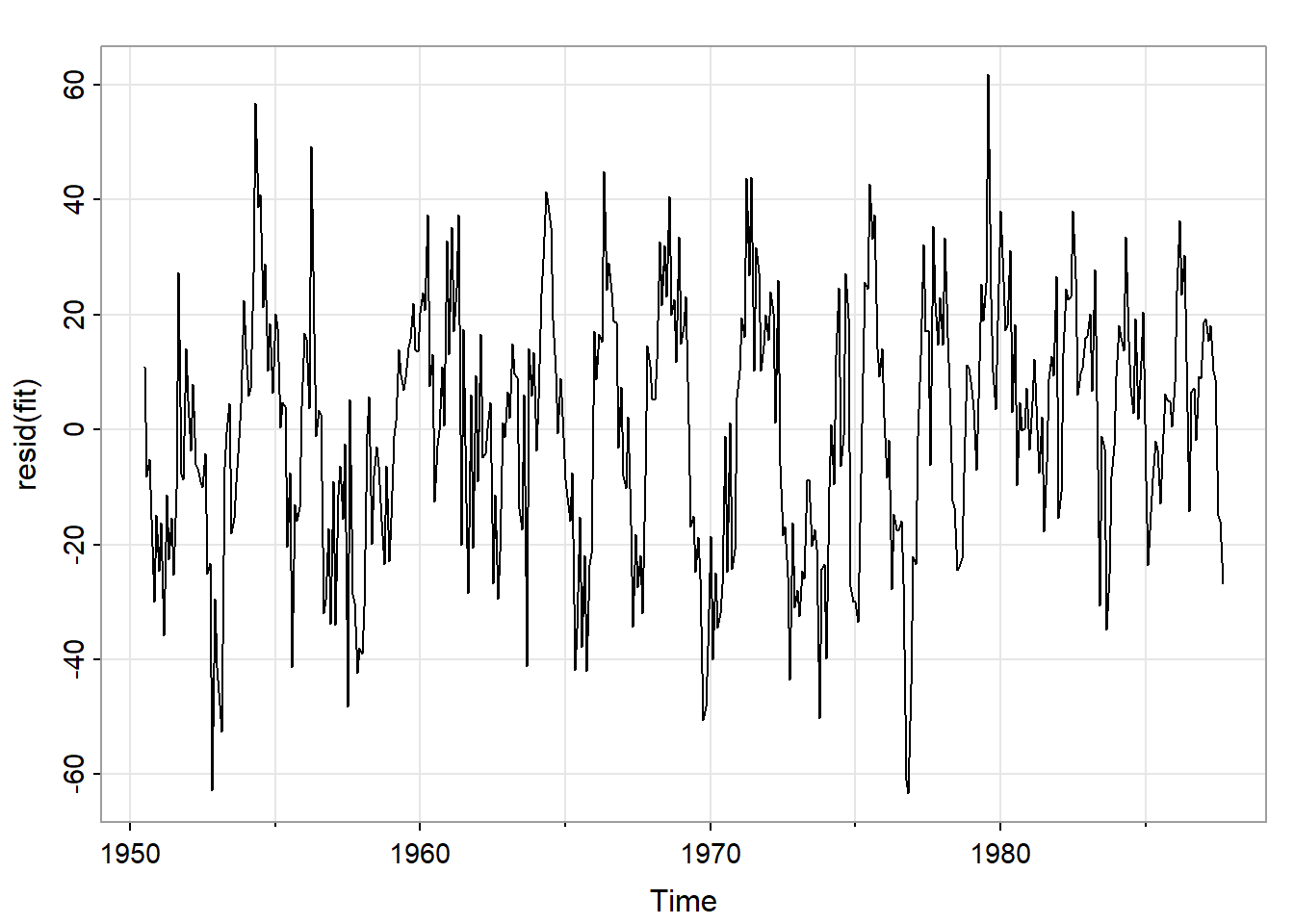
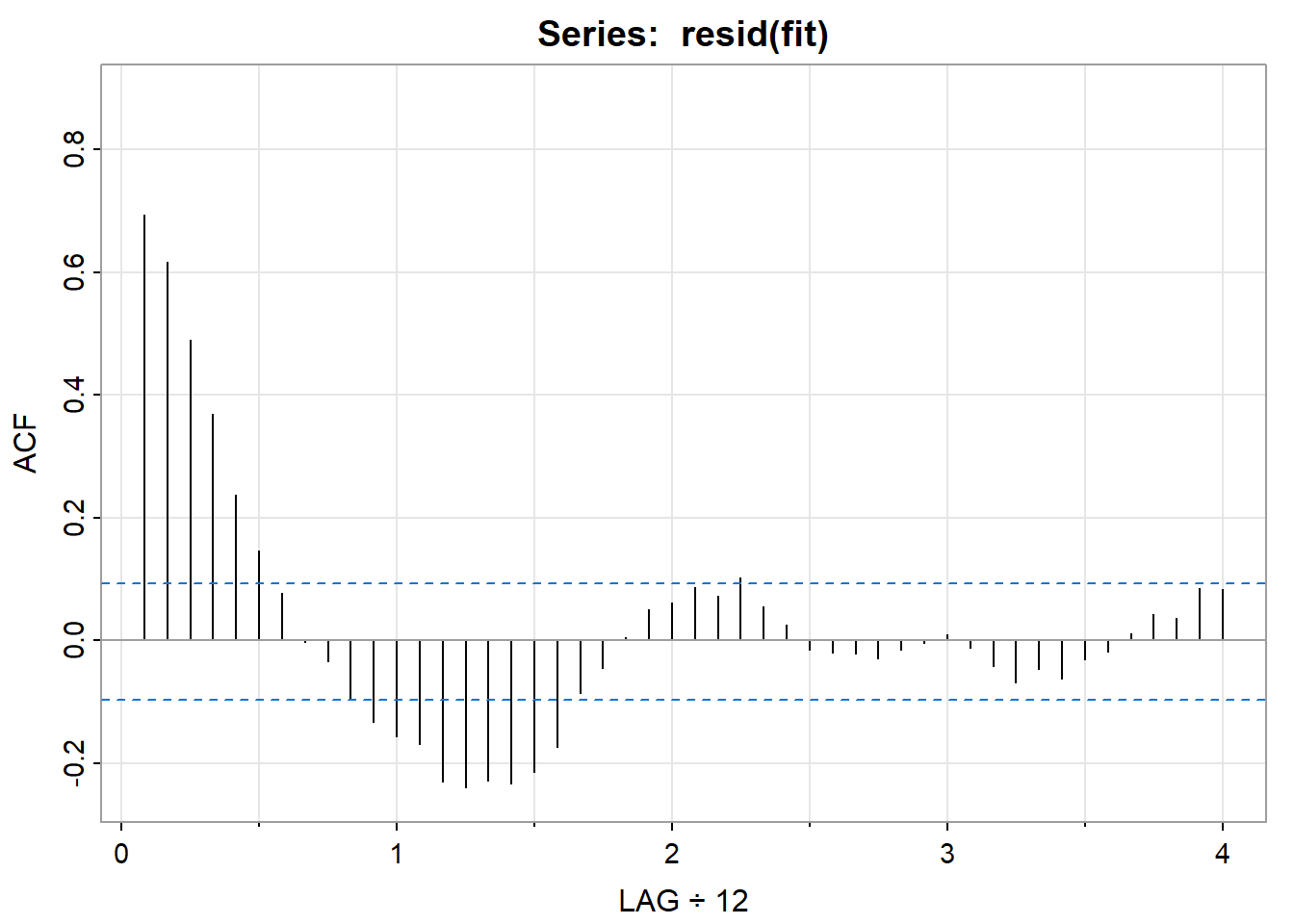
可见残差不是白噪声,还需要进一步分解,这也在第三章进行讨论。
2.4 使用回归发现噪声中的信号
第一章2.5小节中我们根据下面的模型生成了500个观测值。
\[ x_t=A\cos(2\pi\omega t+\phi)+w_t \]
其中\(\omega=1/50\),\(A=2\),\(\phi=0.6\pi\),\(\sigma_w=5\)。也就是:
\[ x_t=2\cos(2\pi\frac{t+15}{50})+w_t \]
假设\(\omega=1/50\)已知,\(A\)和\(\phi\)是未知参数。可以得到:
\[ A\cos(2\pi\omega t+\phi)=\beta_1\cos(2\pi\omega t)+\beta_2\sin(2\pi\omega t) \]
其中\(\beta_1=A\cos(\phi)\),\(\beta_2=-A\sin(\phi)\)。
set.seed(90210)
x = 2 * cos(2 * pi * 1:500 / 50 + 0.6 * pi) + rnorm(500, 0, 5)
z1 = cos(2 * pi * 1:500 / 50)
z2 = sin(2 * pi * 1:500 / 50)
sum_fit = summary(fit <- lm(x ~ 0 + z1 + z2))
sum_fit
Call:
lm(formula = x ~ 0 + z1 + z2)
Residuals:
Min 1Q Median 3Q Max
-14.8584 -3.8525 -0.3186 3.3487 15.5440
Coefficients:
Estimate Std. Error t value Pr(>|t|)
z1 -0.7442 0.3274 -2.273 0.0235 *
z2 -1.9949 0.3274 -6.093 0.00000000223 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5.177 on 498 degrees of freedom
Multiple R-squared: 0.07827, Adjusted R-squared: 0.07456
F-statistic: 21.14 on 2 and 498 DF, p-value: 0.000000001538得到\(\hat\beta_1\)为-0.744,\(\hat\beta_2\)为-1.995。而实际值为\(\beta_1=2\cos(0.6\pi)\approx-0.62\)和\(\beta_2=-2\sin(0.6\pi)\approx-1.90\)。可见即使信噪比很小,我们也可以使用回归找出其中的信号。图 18展示了拟合结果。
tsplot(x, col=astsa.col(4,.7), ylab=expression(hat(x)))
lines(fitted(fit), col=2, lwd=2)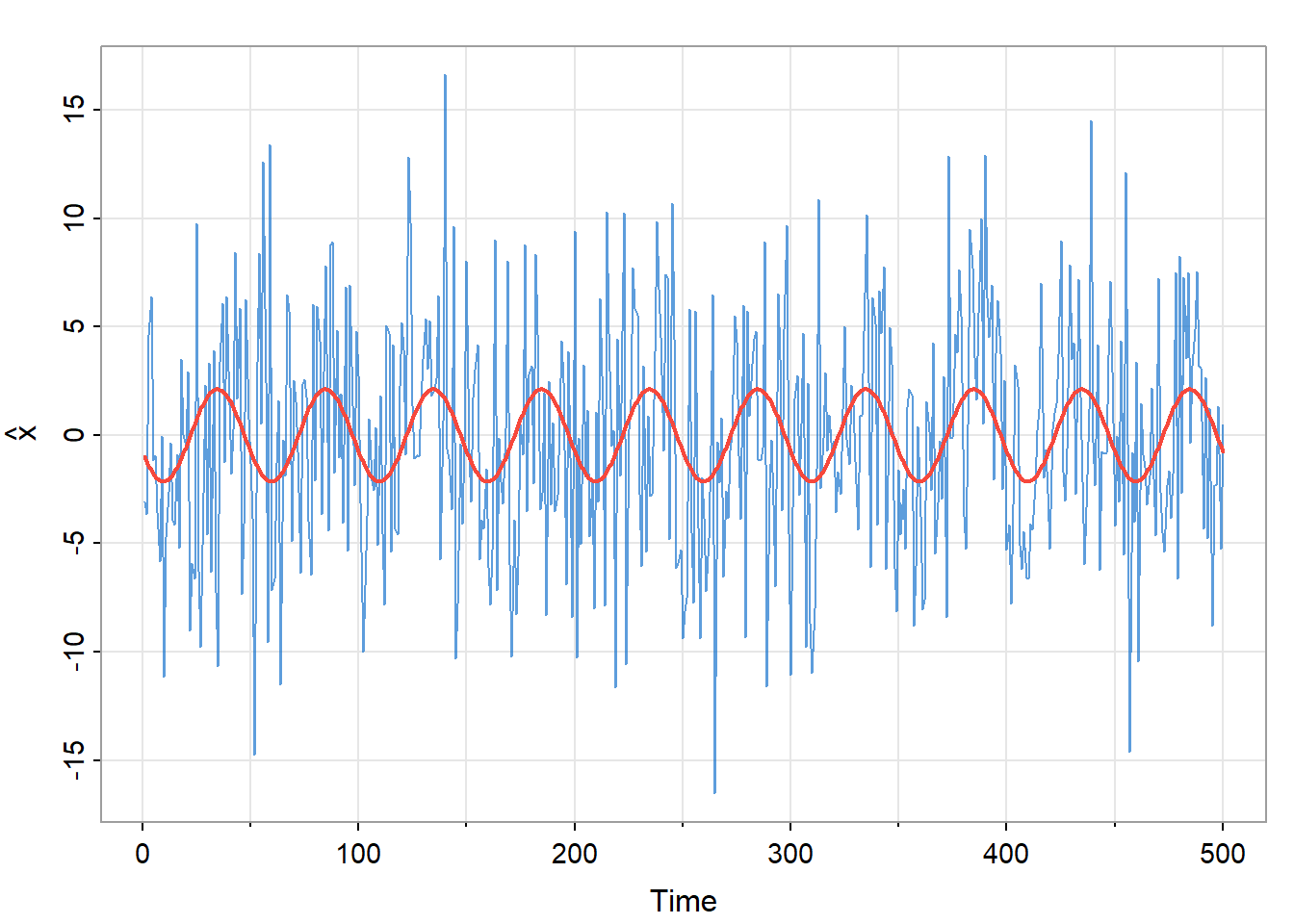
3 时间序列中的平滑
3.1 移动平均平滑
\(x_t\)为观测值,那么
\[ m_t=\sum_{j=-k}^k a_jx_{t-j} \tag{12}\]
是数据的对称移动平均值,其中\(a_j=a_{-j}\ge0\)且\(\sum_{j=-k}^k a_j=1\)。
式 12可以理解为\(x_t\)及其前\(k\)个和后\(k\)个数据加权后取平均,且加权值是对称的。
图 19展示了月度SOI序列,使用式 12进行平滑,权重为\(a_0=a_{\pm1}=\cdots=a_{\pm5}=1/12\),\(a_{\pm6}=1/24\),\(k=6\)。这种方法消除了明显的年度温度循环,有助于强调厄尔尼诺循环。
\(k=6\)差不多涵盖了一年,\(a_{\pm6}=1/24\)让一年边缘的数值更小,可以减缓年度变换的波动。
wgts = c(.5, rep(1,11), .5)/12
soif = stats::filter(soi, sides=2, filter=wgts)
tsplot(soi, col=4)
lines(soif, lwd=2, col=6)
par(fig = c(.75, 1, .75, 1), new = TRUE)
nwgts = c(rep(0,20), wgts, rep(0,20))
plot(nwgts, type="l", ylim = c(-.02,.1), xaxt='n', yaxt='n', ann=FALSE)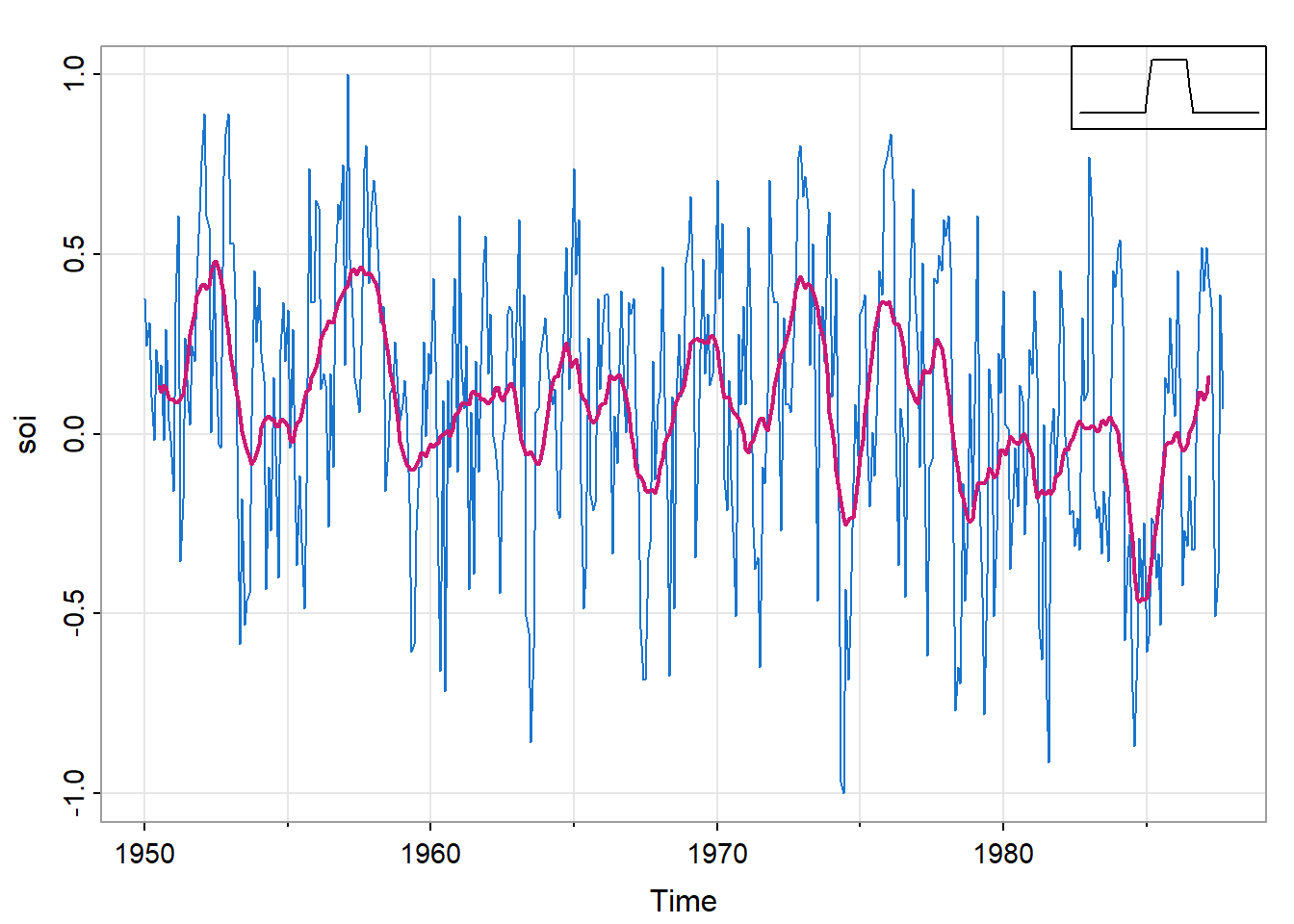
图 19右上角展示了{#eq-2_37}“boxcar”类型权重的形状(未按比例绘制)。
这种处理方法可以突出厄尔尼诺现象,但看起来波动太大,可以使用正态分布权重来获得更平滑的拟合。
3.2 核平滑(Kernel Smoothing)
核平滑是一种移动平均平滑器,使用权重函数或核函数来平均观测值。
\[ m_t=\sum_{i=1}^nw_i(t)x_i \]
其中
\[ w_i(t)=K\left(\frac{t-i}{b}\right)\bigg/\sum_{j=1}^nK\left(\frac{t-j}{b}\right) \tag{13}\]
是权重,\(K(\bullet)\)是核函数。实例中我们常用的是正态核\(K(z)=\frac{1}{\sqrt{2\pi}}\exp(-z^2/2)\)。
R中可以使用ksmooth函数来实现核平滑。
ksmooth(x, # 通常是时间
y, # 值
kernel = c("box", "normal"), # 核函数的类型
bandwidth, # 带宽
range.x, # 自变量的取值范围
n.points = 100) # 输出的平滑曲线上的点的数量带宽是式 13中的\(b\),其作用是对核进行缩放,使四分位数为0.25*带宽,带宽越大,平滑效果越强,趋势越明显,但细节可能被忽略;带宽越小,平滑程度越弱,噪声保留得更多。标准正态分布的四分位数约为\(\pm0.674\)。
图 20展示了\(b=1\)对应一年的平滑。
tsplot(soi, col=4)
lines(ksmooth(time(soi), soi, "normal", bandwidth=1), lwd=2, col=6)
par(fig = c(.75, 1, .75, 1), new = TRUE)
curve(dnorm, -3, 3, xaxt='n', yaxt='n', ann=FALSE)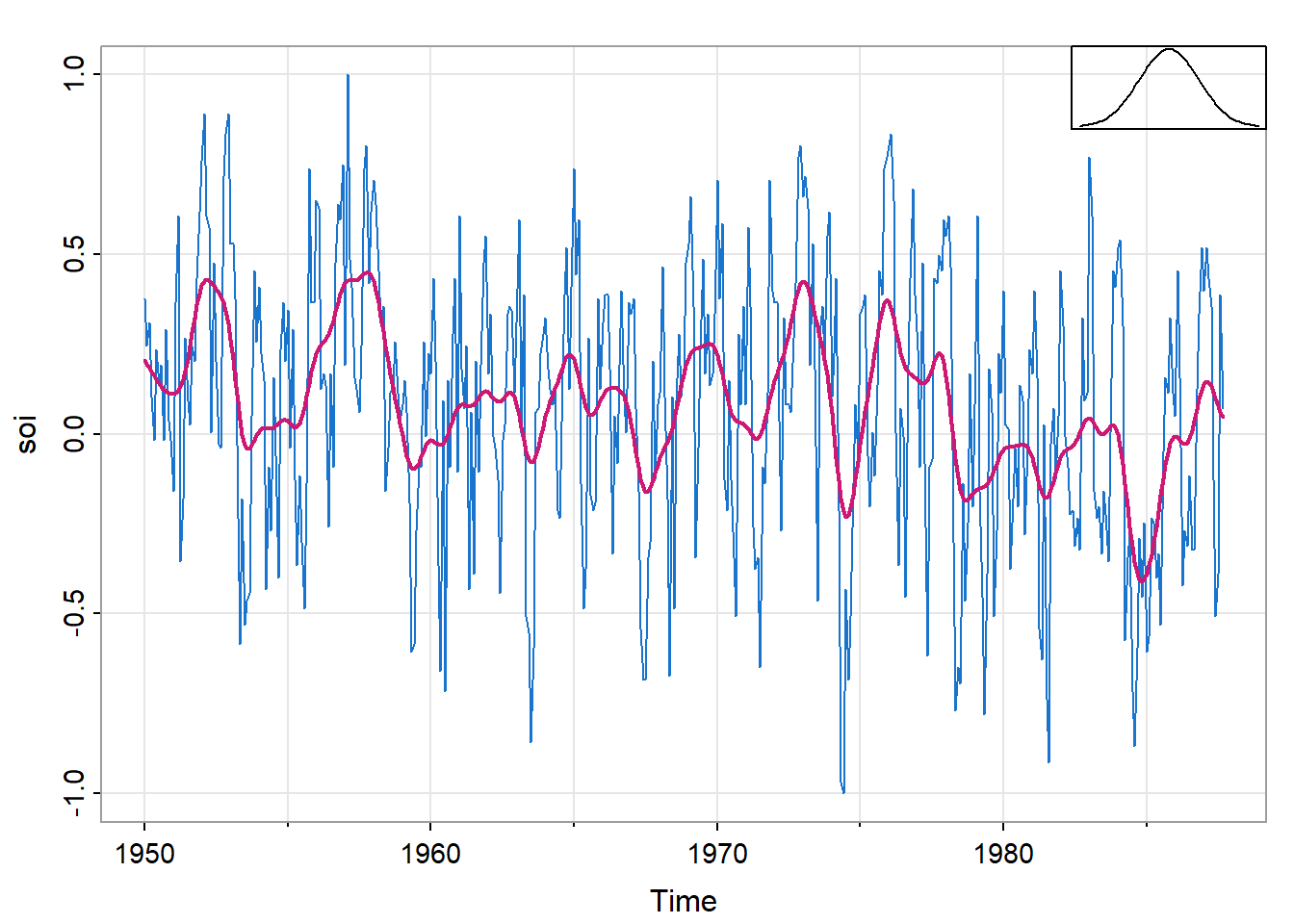
3.3 lowess
平滑时间图的另一种方法是最近邻回归(nearest neighbor regression)。简单来说\(k\)-最近邻回归就是使用\(\{x_{t-k/2},\ \cdots,\ x_t,\ \cdots,\ x_{t+k/2}\}\)进行回归来预测\(x_t\),然后设置\(m_t=\hat x_t\)。
lowess是一种很复杂的平滑方法,但基本思想类似最近邻回归。lowess通过局部加权回归拟合每个数据点的邻域。在每个点周围选择一定比例的相邻点,给这些点赋予权重,离中心点越近的点权重越大,离得越远的点权重越小。然后在该局部范围内拟合一个线性回归模型,并用这个局部模型预测当前点的平滑值。
R中可以使用lowess函数来实现核平滑。
lowess(x,
y,
f = 2 / 3, # 平滑参数,控制平滑的程度。
iter = 3, # 迭代次数,用于减少异常值的影响
delta = 0.01 * diff(range(x))) # 一个用于减少计算量的参数,但对结果的精确度影响很小f值表示选取周围占整体数据比重多少的值进行估计。
较大的f值会使用更多的邻域点,生成较为平滑的曲线,适合总体趋势比较平缓的数据。
较小的f值会使用更少的邻域点,生成较为敏感的曲线,更好地捕捉局部细节和急剧变化,但容易受到噪声的影响。
trend(soi, lowess=TRUE)
lines(lowess(soi, f=.05), lwd=2, col=6)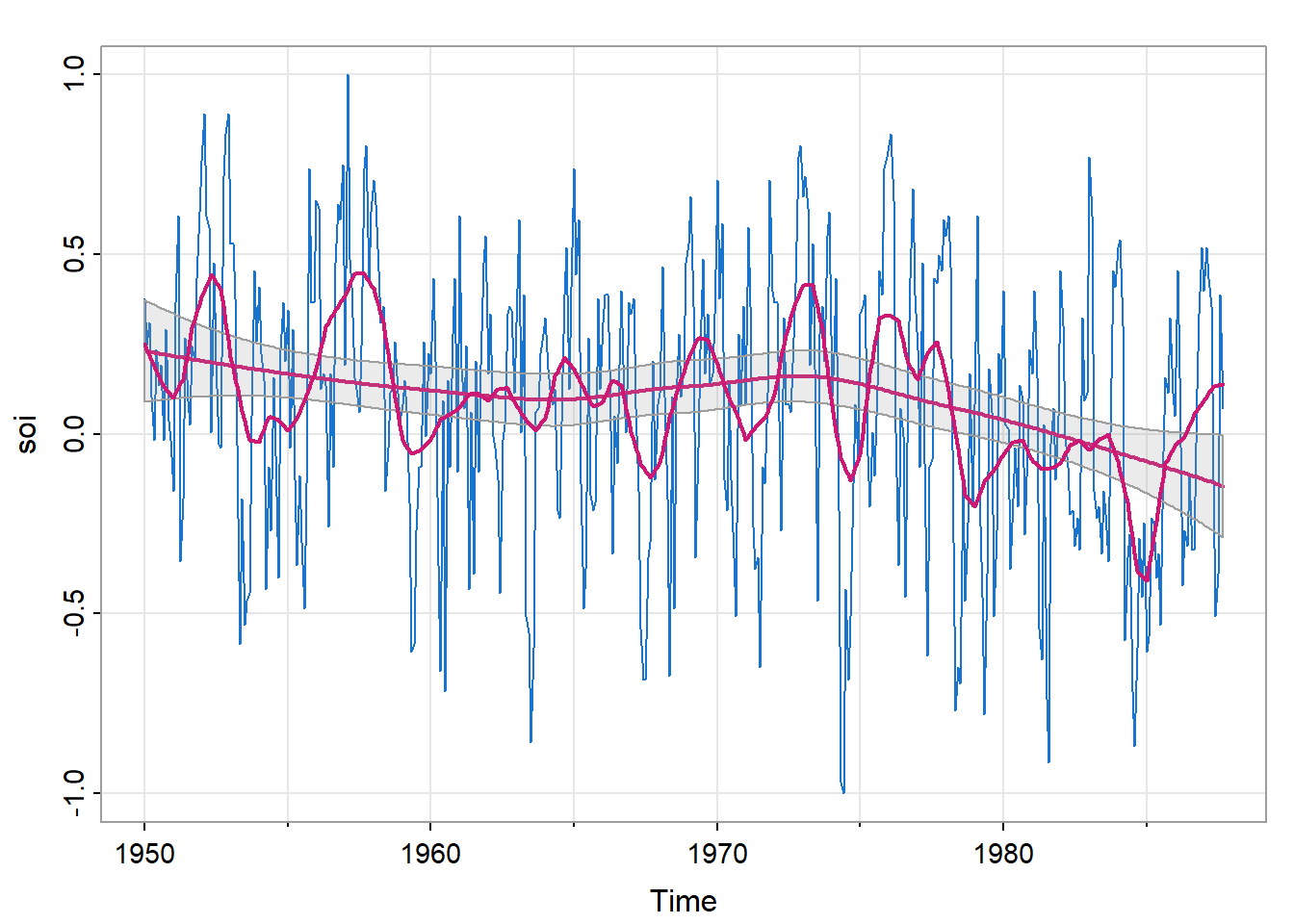
图 21中,较为平缓的线是\(f=2/3\)默认值时的情况,较为曲折的线是\(f=0.05\),即使用5%数据获得估计值时的情况。前者可以观察到太平洋长期变暖,后者可以观察厄尔尼诺现象。
3.4 平滑样条(Smoothing Splines)
平滑样条的核心思想是通过最小化一个损失函数来找到一条平滑的曲线,该损失函数可以兼顾数据的拟合度和曲线的光滑性。
使用平滑样条进行平滑,首先是使用一个和时间\(t\)相关的三次项\(m_t\)来估计\(x_t\)。即:
\[ m_t=\beta_0+\beta_1t+\beta_2t^2+\beta_3t^3 \]
而\(x_t=m_t+w_t\)。
在此基础上,将时间划分进\(k\)个区间,即\([t_0=1,t_1],\ [t_1+1,t_2], \cdots,\ [t_{k-1}+1,t_k=n]\)。\(t_0,\ t_1,\ \cdots,\ t_k\)被成为节点(knot)。在每个区间中进行上述的拟合,因为阶数为3,所以叫三次样条(cubic splines)。
之后是构建损失函数:
\[ \sum_{t=1}^n[x_t-m_t]^2+\lambda\int(m_t'')^2\operatorname{d}t \]
其中\(m_t\)是每个\(t\)组成的区间里的三次样条,\(\lambda>0\)。
用开车来理解公式,\(m_t\)就是车在时间\(t\)处的距离,\(m_t''\)就是瞬时加速度,\(\int(m_t'')^2\operatorname{d}t\)反映了加速和减速的总量,越小说明速度越平缓,反映到函数上就是越平滑。\(\lambda\)是加速和减速的总量的权重,主要进行调整的参数。
\(\sum_{t=1}^n[x_t-m_t]^2\)部分表示拟合,\(\lambda\int(m_t'')^2\operatorname{d}t\)部分表示平滑程度,两者之和最小就是在当前\(\lambda\)下拟合和平滑程度整体的最优解。
R中可以使用smooth.spline函数来实现lowess。
smooth.spline(x, y,
spar = NULL, # 平滑参数,控制平滑程度(不等于$\lambda$)
df = NULL, ...) # 自由度,控制平滑度的另一种方式,spar和df不能同时使用更多信息使用?smooth.spline查看。
图 22中直线spar值为0.5,虚线spar值为1。
tsplot(soi)
lines(smooth.spline(time(soi), soi, spar=0.5), lwd=2, col=4)
lines(smooth.spline(time(soi), soi, spar= 1), lty=2, lwd=2, col=2)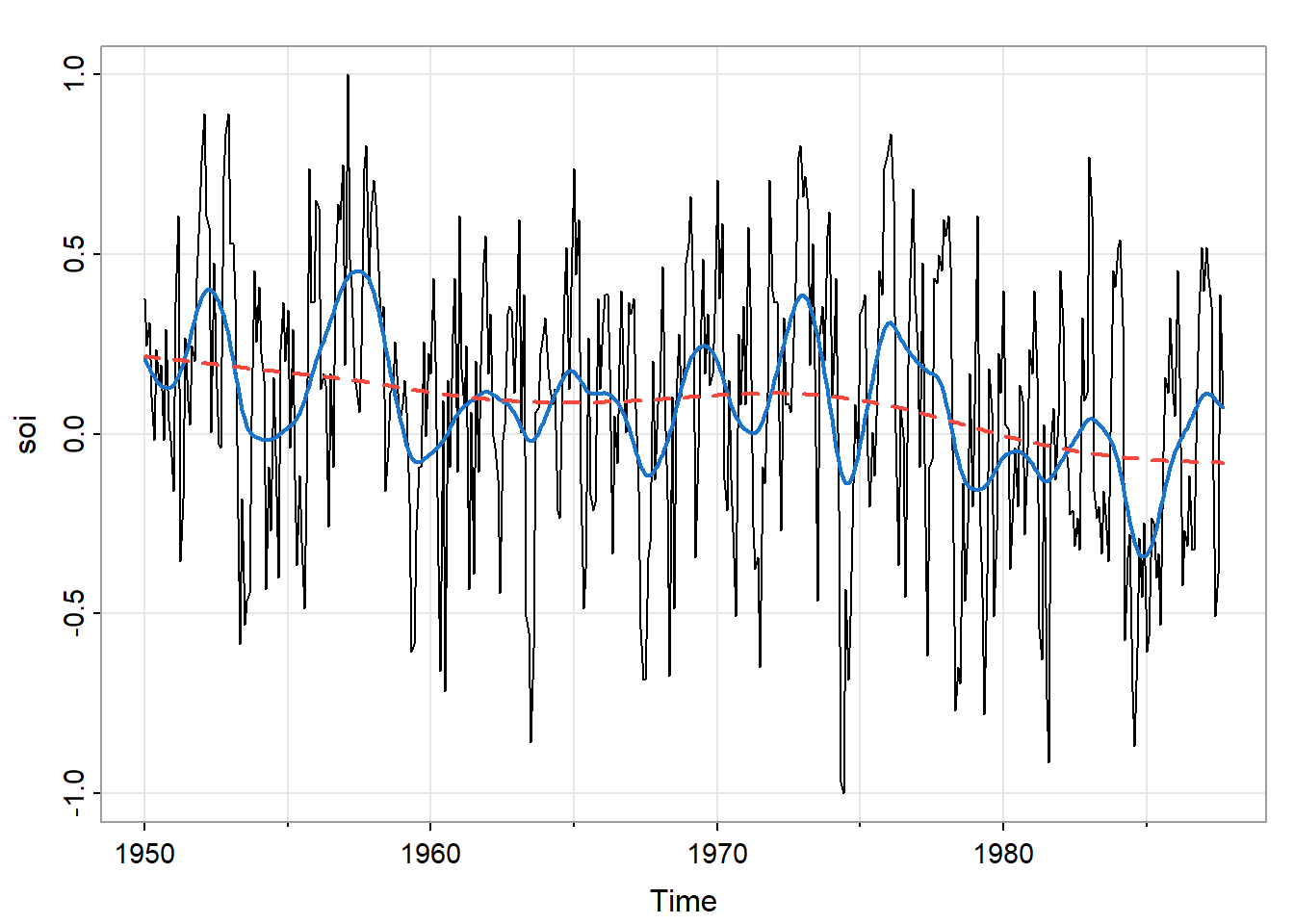
3.5 平滑一个序列作为另一个序列的函数
使用小节 1.2.2中的例子进行展示。图 23是用lowess平滑的\(M_t\)作为\(T_t\)的函数。
tsplot(tempr, cmort, type="p", xlab="Temperature", ylab="Mortality", pch=20, col=4)
lines(lowess(tempr, cmort), col=6, lwd=2)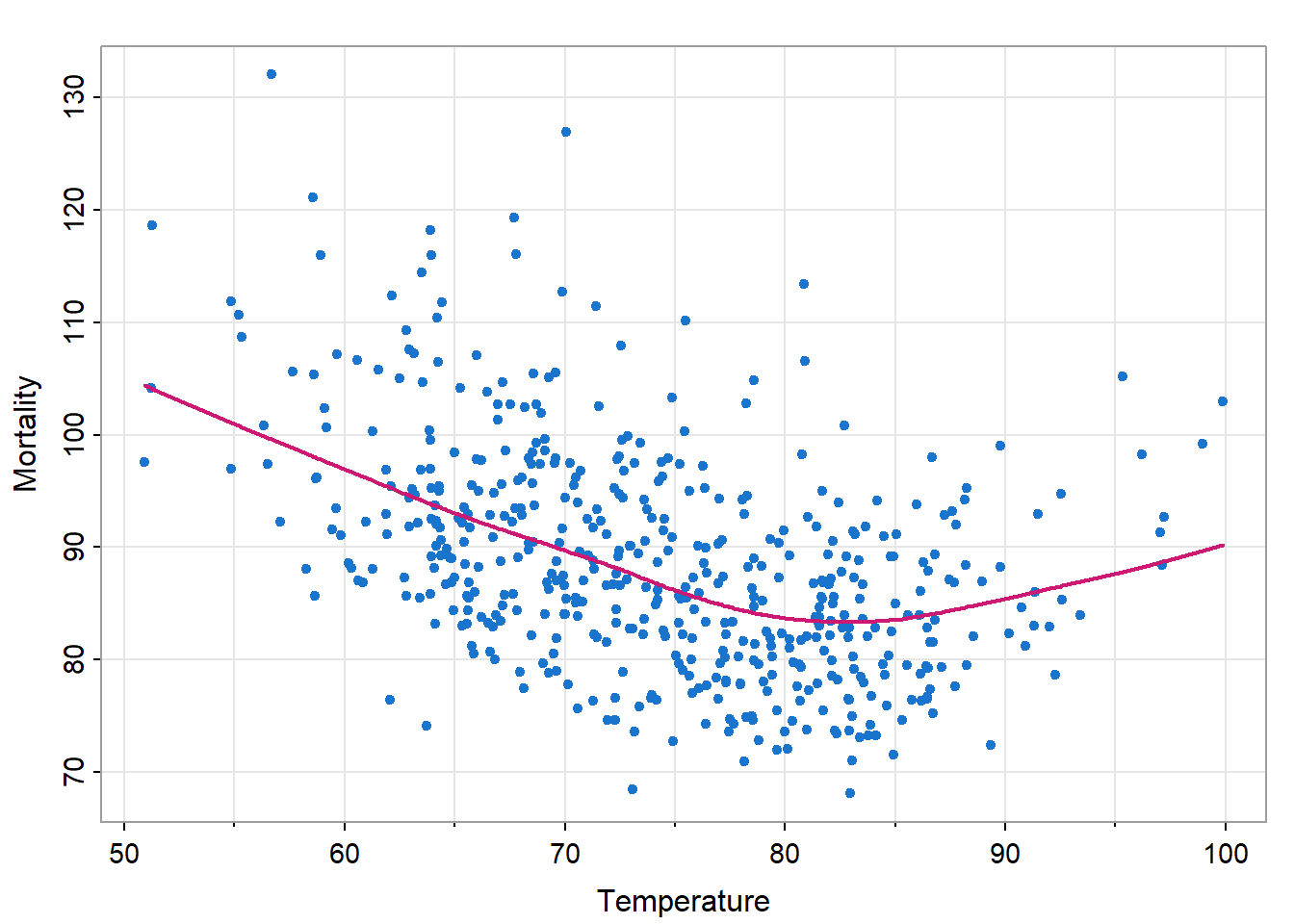
可见在极端温度下死亡率会增高,且极端低温死亡率高于极端高温,最低死亡率出现在80-90℉之间。