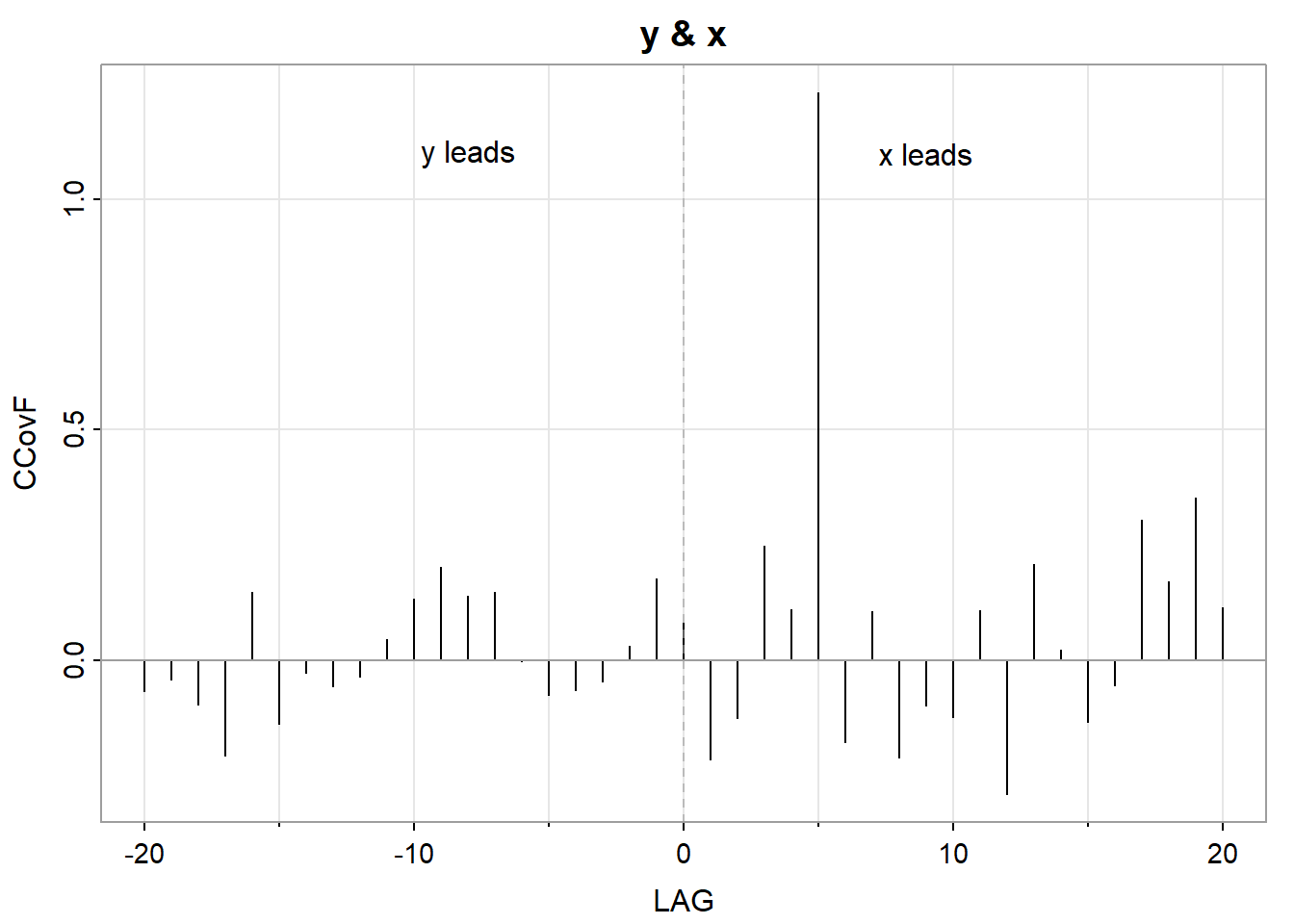给出补充的推导过程帮助记忆和理解。
注意:\(\gamma_{xy}(h)\)等于\(\operatorname{cov}(x_{t+h},y_t)\),而不是等于\(\operatorname{cov}(x_t,y_{t+h})\),在自协方差里面混淆了不影响结果,但在交叉协方差里面是有影响的。
- 方差
因为是独立随机变量,所以\(\operatorname{cov}(w_t,w_{t-1})=0\),所以:
\[
\gamma_x(0)=\operatorname{var}(x_t)=\operatorname{var}(w_t+w_{t-1})=\operatorname{var}(w_t)+\operatorname{var}(w_{t-1})+2\operatorname{cov}(w_t,w_{t-1})=2\sigma_w^2
\]
同理:
\[
\gamma_y(0)=\operatorname{var}(y_t)=\operatorname{var}(w_t-w_{t-1})=\operatorname{var}(w_t)+\operatorname{var}(w_{t-1})-2\operatorname{cov}(w_t,w_{t-1})=2\sigma_w^2
\]
- 滞后自协方差
\[
\begin{aligned}
\gamma_x(1)=\operatorname{cov}(x_{t+1},x_t)
&=\operatorname{cov}(w_{t+1}+w_t,w_t+w_{t-1})\\
&=\operatorname{cov}(w_{t+1},w_t)+\operatorname{cov}(w_{t+1},w_{t-1})+\operatorname{cov}(w_t,w_t)+\operatorname{cov}(w_t,w_{t-1})\\
&=0+0+\sigma_w^2+0\\
&=\sigma_w^2
\end{aligned}
\]
类似的:
\[
\begin{aligned}
\gamma_y(1)=\operatorname{cov}(y_{t+1},y_t)
&=\operatorname{cov}(w_{t+1}-w_t,w_t-w_{t-1})\\
&=\operatorname{cov}(w_{t+1},w_t)-\operatorname{cov}(w_{t+1},w_{t-1})-\operatorname{cov}(w_t,w_t)+\operatorname{cov}(w_t,w_{t-1})\\
&=0-0-\sigma_w^2+0\\
&=-\sigma_w^2
\end{aligned}
\]
- 自协方差
\[
\gamma_x(h)=\begin{cases}
2\sigma_w^2&h=0\\
\sigma_w^2&|h|=1\\
0&|h|\ge2\\
\end{cases}
\]
\[
\gamma_y(h)=\begin{cases}
2\sigma_w^2&h=0\\
-\sigma_w^2&|h|=1\\
0&|h|\ge2\\
\end{cases}
\]
交叉相关函数是在式 10的基础上,简单的公式代入,不做补充推导。