# 检索局部正峰值
cluster -i ${1} --mm -n 100000 --olmax=${1}_pos.txt -t 0.1
# 创建一个负图像便于之后提取负峰值
fslmaths ${1} -mul -1 ${1}_neg.nii.gz
# 检索局部负峰值
cluster -i ${1}_neg --mm -n 100000 --olmax=${1}_neg.txt -t 0.1
# 移除负图像
rm ${1}_neg.nii.gzSDM-PSI参考手册
1 介绍
Seed-based d Mapping (以前称为Signed Differential Mapping) with Permutation of Subject Images (即SDM-PSI) 是一种使用神经成像技术 (如fMRI、VBM、DTI或PET) 对脑活动或结构差异进行元分析研究的统计技术。它也可以指由SDM项目组开发的一款用于进行这种元分析的特定软件。
1.1 方法概述
SDM采用并结合了以往方法 (如ALE或MKDA) 的多种优良特性，并引入了一系列改进和新特性。为避免在同一个体素中同时出现正负结果 (这是以前方法中常见的问题) ，引入了一项新特性，即在同一张图中表示正差异和负差异，从而获得了signed differential map (“SDM”) 。在2.11版本中引入的另一项重要改进是效应量的使用 (effect-size SDM或“ES-SDM”) ，这使得可以将报告的峰值坐标 (peak coordinates) 与统计参数图 (statistical parametric maps) 相结合，从而进行更全面和更精确的元分析。另一项改进是在4.11版本中引入的，使用各向异性内核 (anisotropic kernels) 在重建效应量图 (effect size images) 时考虑空间协方差的各向异性。
在6.11版本中，实施了这一方法的新一代技术 (结合Permutation of Subject Images的SDM，即SDM-PSI) 。SDM-PSI的一些新特性包括：
基于MetaNSUE算法的 (几乎) 无偏效应量估计(Albajes-Eizagirre, Solanes, & Radua, 2019)。
使用常见的置换检验进行多重比较的Familywise校正，即permuting subject images (PSI) 。需要注意的是，以前的方法使用的是空间收敛性检验 (tests for spatial convergence) ，这些检验依赖于空间假设，而这些假设可能不成立，并且在存在多重效应时统计功效较低(Albajes-Eizagirre & Radua, 2018)。
Freedman-Lane-based permutation，因其最佳的统计特性而选用(Winkler et al., 2014)。
Threshold-free cluster enhancement (TFCE) ，在模拟研究中，这种统计方法既不过于保守，也不过于宽松 (而基于体素的统计过于严格，基于簇的统计则过于宽松) (Smith & Nichols, 2009)。
该方法分为五步。首先，根据SDM的纳入标准，选择簇峰的坐标 (如：患者与健康对照者之间差异最大的体素) 以及统计图 (如果有的话) 。其次，对于只有峰坐标的研究，估计可能的效应量图的上下限。第三，使用MetaNSUE来估计最可能的效应量及其标准误，并通过在这些估计值中加入噪声，在上下限范围内生成多个插补。第四，分别对每个插补的数据集进行元分析，然后使用Rubin’s rules将这些插补的元分析数据集合并。最后，重建主体图像，以便运行标准置换检验 (standard permutation test) ，在每一组置换的图像上重复该过程，并保存最终图像的最大统计值；这些最大值的分布用于对多重比较进行family-wise误差校正。
1.2 峰值坐标的包含准则
在神经影像学研究中，某些大脑区域 (如先验的关注的区域) 常常会使用比其他区域更宽松的阈值标准进行分析。这种做法并不罕见。然而，如果在元分析中包含了这种研究内存在区域阈值差异的研究，那么结果可能会偏向这些区域，因为这些区域可能仅仅因为研究者在其上应用了更宽松的阈值而更容易被报告出来。为了解决这个问题，SDM引入了一种坐标选择标准，可以概括为：
“尽管不同的研究可能使用不同的阈值，但在纳入的每一个研究内，应该确保整个大脑使用相同的阈值”。
1.3 研究的预处理
统计参数图的预处理相对简单，它们会被直接配准到SDM模板上，并将\(t\)值转换为效应量。对于仅有峰值坐标的研究，则为每个研究在特定的掩膜 (mask) 内 (如灰质体积、皮层厚度、白质、TBSS、脑脊液等) 创建可能效应量的上下阈图。这是通过各向异性非归一化的高斯核 (anisotropic un-normalized Gaussian Kernel) 来实现的，依据特定的灰质、白质、分数各向异性或脑脊液相关模板，使得与峰值坐标相关性更高的体素具有与峰值相似的效应量。在每个研究内，由接近各向异性核得到的值通过平方距离加权平均进行组合。
1.4 统计比较
SDM提供了几种不同的统计分析方法，以通过敏感性和异质性分析来补充主要结果。
主要的统计分析是均值分析，其过程是计算不同研究中体素值的平均值。该平均值会通过方差的倒数进行加权，并考虑研究间 (inter-study) 的异质性。
亚组分析是应用于研究组的均值分析，以便研究异质性。
线性模型分析 (如元回归) 是均值分析的广义形式，允许组间比较和潜在混杂因素的研究。
这些分析的统计显著性通过未经校正的\(p\)值或FWER校正的\(p\)值来评估。还可以提取原子标签 (atomical label) 或坐标中的值以进行进一步处理或图形化表示。
1.5 SDM软件
SDM是由SDM项目组开发的软件，用于帮助基于体素的神经成像数据的元分析。它作为免费软件发布，包括命令行和图形界面。
2 准备工作
提取的神经影像数据必须包含在一个文件夹里 (参见小节 2.1) ，样本、组别或变量的信息必须在SDM表格中输入 (参见小节 2.2) 。准备工作的最后一步是对研究数据进行预处理以及蒙特卡洛随机化 (参见小节 2.3) ，如果是TBSS元分析，还需要执行一系列特殊步骤 (参见小节 2.4) 。
2.1 准备文件夹
SDM软件假设元分析所需的所有文件都在同一个文件夹中。
2.1.1 图像文件
如果有群体水平 (group-level) 的统计参数图可用，强烈建议使用这些图像文件而不是峰值坐标。这些图像文件必须是NIfTI格式的，并且可以通过SDM的“Convert images”功能轻松适配。注意从其他软件转换的NIfTI文件有时可能会失效，例如，可能导致空白图像或翻转图像。因此，我们强烈建议使用脑图查看器 (如MRICron、FSLView或SPM Display) 进行以下检查：
转换后的文件是否为正确的大脑图像。
左右两侧是否未翻转。
预处理的峰值是否与文献中报告的峰值相似。
如果转换失败，你可以尝试首先将原始NIfTI文件复制到元分析目录中，然后用MRICron打开并保存该副本，最后用SDM进行转换。这似乎能修复SDM无法正确转换文件的小问题。
如果左右两侧翻转，您可以尝试使用FSL (“fslswapdim [filename] -x y z [filename]”) 、MRICro (“Save as…”: “Flip Left/Right”) 或SPM (“Display”: “resize {x} = -1”) 修复问题。
2.1.2 文本文件
每项研究的峰值坐标必须写入文本文件，文件名应为研究名称加上以下扩展名之一：
.spm_mni.txt：SPM坐标在MNI空间中 (如Walker2004.spm_mni.txt)；.spm_brett.txt：使用Brett转换将SPM坐标从MNI空间转换到Talairach空间 (如Brown2009.spm_brett.txt)；.spm_tal.txt：SPM坐标在正确的Talairach空间中 (如Williams1999.tal.txt)。这种情况很少见或仅用于特殊分析，请务必确认是否应使用.spm_mni.txt或.spm_brett.txt；.fsl_mni.txt：FSL坐标在MNI空间中 (如Walker2004.spm_mni.txt)；.fsl_brett.txt：使用Brett转换将FSL坐标从MNI空间转换到Talairach空间 (如Taylor2002.spm_brett.txt)；.fsl_tal.txt：FSL坐标在正确的Talairach空间中 (如Davies2013.tal.txt)。这种情况很少见或仅用于特殊分析，请务必确认是否应使用.fsl_mni.txt或.fsl_brett.txt；.other_mni.txt：非FSL坐标和SPM坐标在MNI空间中 (如Hall2004.spm_mni.txt)；.other_brett.txt：使用Brett转换将非FSL坐标和SPM坐标从MNI空间转换到Talairach空间 (如Evans2005.other_brett.txt)；.other_tal.txt：非FSL坐标和SPM坐标在正确的Talairach空间中 (如Wright2004.tal.txt)。
提示
这部分完全按照原文翻译的，命名的示例应该是有问题的。
每个坐标必须按照以下格式写成一行：x,y,z,t，其中t要么是正的\(t\)值或’p’(正差异，如激活，对照组>控制组)，要么是负的\(t\)值或’n’(负差异，如去激活，对照组<控制组)。示例如下：
-8, 46, 3, 3.42
12, 2, 2, -4.43
18, 22, 4, n
你可以通过在线的Convert peaks utility，轻松将p值和z分数转换为\(t\)值。
2.1.3 指定文件夹
点击Change meta-analysis
或
在Meta-analyses菜单中选择Change meta-analysis
2.2 创建SDM表
纳入元分析的研究的名称、患者组的样本量和使用的阈值，必须在SDM表的列中指定。你还可以指定其他变量，这些变量将在后续计算中作为指标、回归量或筛选条件。
2.2.1 创建或编辑表
点击SDM table editor按钮
或
在Meta-analyses菜单中选择SDM table editor打开下面内容：
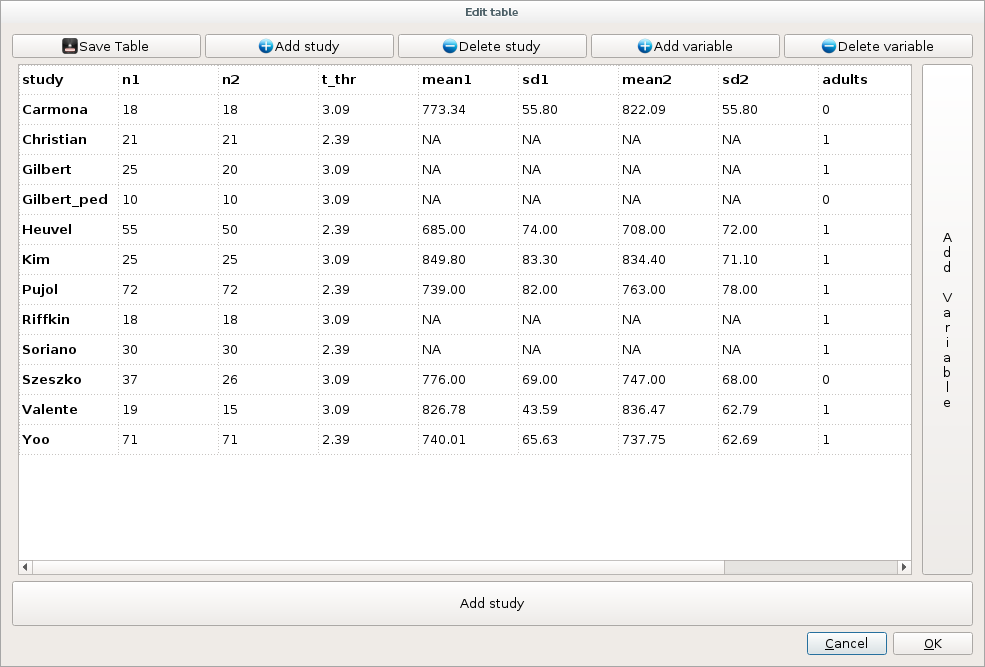
2.2.2 表的主要列
n1 (必须有)：主要样本的大小，如每个研究中患者人数。
n2 (仅适用于两样本对比)：对照样本的大小，如每个研究中健康控制组人数。
t_thr：研究中用于threshold maps的值。
mean1和sd1 (仅适用于全局过程)：主要样本中全局测量的平均值 (和标准差)，如患者的全局灰质。
mean2和sd2 (仅适用于两样本对比时的全局过程)：对照样本中全局测量的平均值 (和标准差)。
2.2.3 备选方案
SDM表保存在一个名为sdm_table.txt的文本文件中，因此你可以使用任何文本编辑器或如Microsoft Excel一样的其他软件创建或修改它。这种情况下，建议之后使用SDM软件中的表格编辑器打开新表格以确保该表格被正确识别。
2.3 预处理
这是准备工作的最后一步。对于峰值坐标研究，需要计算每个体素可能效应量的下界和上界图像。对于原始图像可用的研究，当需要时，唯一需要执行的步骤是将原始图像转换为效应量图像。
2.3.1 对研究进行预处理
点击Preprocessing
或
在Meta-analyses菜单中选择Preprocessing打开下面内容：
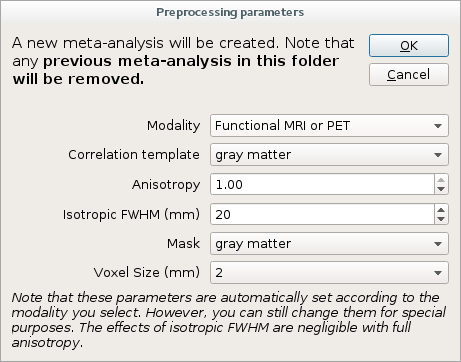
2.3.2 注意事项
请注意，这将删除此文件夹中之前的元分析。
每项研究的最大值和最小值将被写入一个名为pp.htm的文本文件(注意：这些值可能不是绝对的最大值和最小值)，而重建的图像将分别保存为一组名为pp_(study).nii.gz的NIfTI文件，如pp_Smith2000.nii.gz。这些文件对于检查坐标是否被正确读取非常有用。
SDM软件中包含了几种尺寸为 ?mm X ?mm X ?mm (其中?是可用的体素大小，目前只有2mm X 2mm X 2mm) 的以MNI为基础的掩膜和相关模板。这些掩膜和模板包括：灰质 (也适用于fMRI和PET)、白质、分数各向异性、脑脊液、大脑及颅内结构。如果需要其他掩膜或模板，请与我们联系。
2.3.3 命令行和批量处理
pp correlation_template,degree_of_anisotropy,isotropic_fwhm,mask,voxel_size
示例：
pp fractional_anisotropy,0.8,20,white_matter,2
提示
pp 相关样本,各向异性程度,各向同性全宽半高,体素大小
2.3.4 参考文献
当前方法：Albajes-Eizagirre, Solanes, Vieta, et al. (2019)
效应量和方差：Radua et al. (2012)
各向异性内核(anisotropic kernels)：Radua, Rubia, et al. (2014)
白质模板：Radua et al. (2011)
TBSS预处理：Peters et al. (2012)
FreeSurfer模板：Li et al. (2020)
2.4 TBSS预处理
来自使用FSL“基于纤维束的空间统计” (TBSS) 的弥散加权 (diffusion-weighted) 研究的统计参数图不能直接使用ES-SDM进行元分析，因为不同研究中的骨架图像不能完全重叠。当然，你总是可以使用包含峰值坐标的文本文件，但应该尽可能优先使用图像。为了确保TBSS研究中的图像与特定的SDM TBSS模板正确重叠，你应该：
首先从原始\(t\)统计图中获取大量低阈值的局部峰值 (参见下方示例)，
然后将正峰值和负峰值合并到同一个电子表格中 (负峰值必须使用负\(t\)值)，
将这些峰值及其\(t\)值保存到一个用于ES-SDM的文本文件中 (参见小节 2.3)，
最后使用TBSS模板进行ES-SDM预处理。
2.4.1 如何使用FSL提取峰值
2.4.2 参考文献
TBSS预处理：Peters et al. (2012)
3 全局分析
你可以对全局变量进行 (相对简单的) 元分析，例如在VBM研究的元分析中分析全局灰质，选择性地调整组别或协变量的影响。
3.1 全局分析
此过程进行全局变量的元分析，例如在VBM研究元分析中分析全局灰质。你可以指定最多2个指示变量来定义组别(即进行3组别比较)、最多2个协变量以及最多1个用于亚组分析的过滤器。统计量使用无偏Hedge’s d，元分析采用限制性最大似然(restricted maximum-likelihood，即Wolfgang Viechtbauer开发的之前可用的MiMa S-Plus或R函数中的默认方法)。
3.2 注意事项
在进行该分析之前，需在SDM表中创建以下变量：
单样本研究 (如健康志愿者对恐惧面孔的脑响应研究)：
n1(样本量)，mean1(关注的全局变量的平均值) 和sd1(关注的全局变量的标准差)。双样本研究 (如比较患者与健康对照组的灰质体积的研究)：
n1和n2(两个样本的大小)，mean1和mean2(关注的变量的平均值)，sd1和sd2(关注的变量的标准差)。
如果在对话框中选择单变量 (如亚组比较或协变量的过滤器)，’0’表示在变量的最小值处估计全局值，’1’表示在变量的最大值处估计全局值，’1m0’表示变量最大值和最小值之间的全局值差异。如果选择双变量，’10’表示第一个变量的最大值和第二个变量的最小值，而’01’表示第一个变量的最小值和第二个变量的最大值，以此类推。
如果选择双变量，还会计算two-variable Q，其含义与ANOVA中的F值类似。
3.3 进行全局分析
点击Globals
或
在Statistics菜单中选择Globals
3.4 命令行和批量处理
globals formula, filter
示例：
GGM = globals
3.5 参考文献
Hedges & Olkin (1985)
4 计算
计算元分析均值 (参见小节 4.1)、包括协变量的组间比较 (参见线性模型分析：组间比较) 和元回归(参见线性模型分析：元回归)。
4.1 均值分析
这个过程计算元分析的平均数。你可以为亚组分析和最多两个协变量指定一个过滤器 (如果使用命令行，则为四个协变量)。
4.1.1 计算平均值
点击Mean
或
在Statistics菜单中选择Mean打开下面对话框：
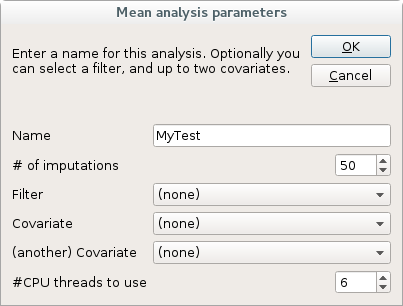
4.1.2 多线程处理
在大规模元分析中，均值计算的最大似然估计 (MLE) 可能需要较长时间，可以使用并行线程来运行。
注意：不建议使用超过你计算机可用线程数量的并行线程。你可以在偏好设置窗口的“多线程”选项卡中查看计算机上的可用线程数量。
4.1.3 命令行和批量处理
mi number_of_imputations,model,filter，其中model是用字符+分隔的协变量列表。
示例：
model_name = mi 50,YBOCS,adults
注意：在使用命令行时，想修改并行线程的数量，需要手动修改在预处理后创建的文件sdmpsi_params.xml中的nthreads值。
4.1.4 参考文献
原始算法：Radua & Mataix-Cols (2009)
效应大小和方差：Radua et al. (2012)
当前方法：Albajes-Eizagirre, Solanes, Vieta, et al. (2019)
4.2 线性模型
线性模型可能在有多个目标时有效，例如对比两组或更多组、控制潜在的混淆因素和通过元回归评估结果的异质性。
4.2.1 线性模型分析
要计算线性模型，你需要指定模型 (最多使用四个变量) 和假设。你还可以为亚组分析指定过滤器。
4.2.2 计算线性模型
点击Linead Model
或
在Statistics菜单中选择Linear Model打开下面对话框：
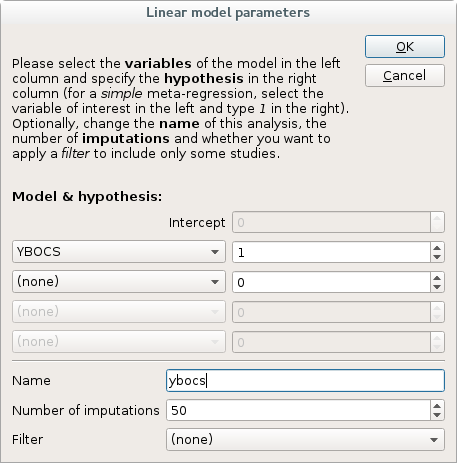### 多线程处理
在大规模元分析中，线性模型计算的最大似然估计 (MLE) 可能需要较长时间，可以使用并行线程来运行。
注意：不建议使用超过你计算机可用线程数量的并行线程。你可以在偏好设置窗口的“多线程”选项卡中查看计算机上的可用线程数量。
4.2.3 命令行和批量处理
mi_lm model,hypothesis,number_of_imputations,filter，其中hypothesis是用字符+分隔的值列表，model是用字符+分隔的协变量列表。
示例：
model_name = mi_lm YBOCS,0+1+0+0+0,50,adults
注意：在使用命令行时，想修改并行线程的数量，需要手动修改在预处理后创建的文件sdmpsi_params.xml中的nthreads值。
4.2.4 参考文献
原始算法：Radua & Mataix-Cols (2009)
比较和线性模型：Radua et al. (2010)
效应大小和方差：Radua et al. (2012)
当前方法：Albajes-Eizagirre, Solanes, Vieta, et al. (2019)
4.3 family-wise error (FWE) 校正
FWE校正是通过运行基于被试的置换检验，以获得最大统计量的分布来实现的。然后，使用该分布对在均值或线性模型计算中获得的元分析图像进行阈值处理，最终得到校正后的 p 值图。
4.3.1 计算FWE
点击FWE
或
在Statistics菜单中选择FWE打开下面对话框：
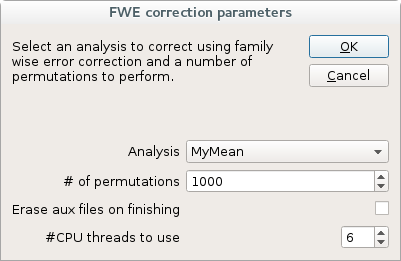
4.3.2 多线程处理
在任何元分析中，FWE计算的分布步骤计算耗时较长，不过可以使用并行线程运行。
注意：不建议使用超过你计算机可用线程数量的并行线程。你可以在偏好设置窗口的“多线程”选项卡中查看计算机上的可用线程数量。
4.3.3 命令行和批量处理
perm number_of_permutations,model_name，其中model_name是之前计算好的平均值或线性模型的名字。
示例：
perm 1000,model_name
注意：在使用命令行时，想修改并发线程数量，需要手动修改计算平均值或线性模型后创建的文件sdmpsi_params.xml中对应模型部分（xml标签）的nthreads值。
4.3.4 参考文献
当前方法：Albajes-Eizagirre, Solanes, Fullana, et al. (2019)
Winkler et al. (2014)
5 结果
可以对先前计算的结果进行阈值化处理，得到元分析峰值坐标、簇分解以及NIFTI图像（Analyze-compatible，参见小节 5.1），这些内容将自动在 MRIcron 模板中打开（参见小节 7）。也可以使用MASK（参见小节 5.2）从 Talairach 标签或坐标中提取结果（参见小节 5.3）。
5.1 阈值化处理结果
相应模型的结果可根据给定的未校正或校正统计显著性水平进行阈值化处理，从而获得峰值坐标、簇分解结果和NIfTI图像。这将会自动打开MRIcron脑成像查看器以显示结果（如果MRIcron已经启动；参见设置来获得关于MRIcron集成的帮助）。
参考文献中 De Schotten et al. (2011) 、Thiebaut de Schotten et al. (2011) 和 Rojkova et al. (2016) 是Catani、Thiebaut de Schotten等人的脑图谱引用信息。
5.1.1 单尾 vs 双尾
和大多数神经成像软件一样，此对话框执行一对单尾检验。为避免假阳性概率翻倍，请将统计显著性水平减半，改为0.025。
5.1.2 阈值化处理图谱
点击Threshold
或
在Statistics菜单中选择Threshold打开下面对话框：
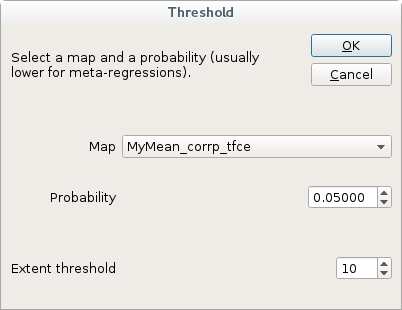
5.1.3 命令行和批量处理
threshold p_map_path,z_map_path,value,minimum number of voxels
示例：
threshold analysis_MyMean/corrp_tfce,analysis_MyMean/MyMean_z,0.05,10
注意：p-map和z-map路径不应该包含扩展名nii.gz。
5.1.4 参考文献
效应大小和方差：Radua et al. (2012)
白质图谱1：De Schotten et al. (2011)
白质图谱2：Thiebaut de Schotten et al. (2011)
白质图谱3：Rojkova et al. (2016)
5.2 MASK的创建
MASK在SDM中用于从所有研究和分析中提取体素或区域中的值。MASK保存在相应模型文件夹（如analysis_model_name）中单独的mask_*.nii.gz文件中。这些文件可以用于多个元分析。
5.2.1 创建MASK
点击Create mask
或
在Tools菜单中选择Create mask打开下面对话框：
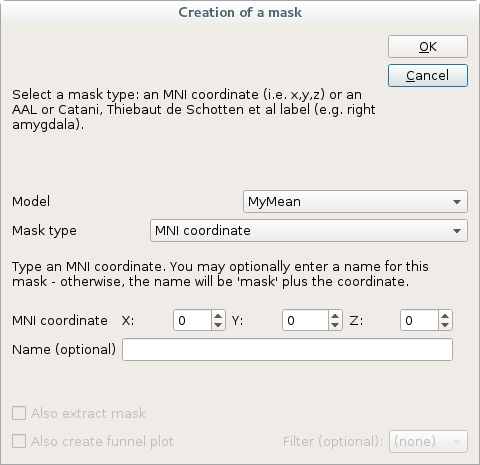
5.2.2 命令行和批量处理
mask model_name,type,numbers
示例：
m25_0_m20 = mask MyMean,coordinate,-25,0,-20 left_amygdala = mask MyMean,label,41
5.2.3 参考文献
白质图谱1：De Schotten et al. (2011)
白质图谱2：Thiebaut de Schotten et al. (2011)
白质图谱3：Rojkova et al. (2016)
5.3 MASK的值的提取
可以从所有研究和分析中提取MASK的值，并将其保存到相应模型的文件夹（如analysis_model_name）中一个名为 extract_(name_of_the_mask).txt 的文本文件中，如extract_left_putamen.txt。该文件可轻松导入Microsoft Excel或类似软件。
5.3.1 提取MASK
点击Extract
或
在Tools菜单中选择Extract打开下面对话框：
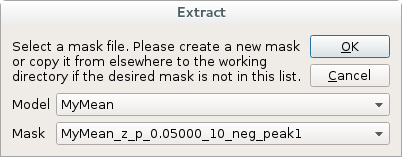
5.3.2 命令行和批量处理
extract model_name,mask file
示例：
extract MyMean,left_amygdala
6 批量处理
为避免重复工作，SDM软件支持简便的批量处理功能，其操作流程为：首先保存某项分析的步骤，然后只需按下一个按钮即可重复执行这些步骤。这对于保存初步分析的步骤并在最终分析中直接重复执行非常有用。
请注意，你也可以使用你最喜欢的语言创建一个脚本并调用SDM。
如./sdm pp gray_matter, 20, 1, gray_matter, 1。
6.1 批量处理（图形界面）
要保存步骤，打开程序，执行各项分析（如预处理、计算、阈值设置、提取等），然后点击Save batch。
要进行批量处理，点击Run Batch。
请注意，当你执行任何分析时，其对应的命令及简短注释会自动添加到SDM batch window。你可以通过修改、添加或删除命令和注释来编辑此窗口内容。完成编辑后，请不要忘记点击Save batch！
6.2 批量处理（控制台界面）
在名为sdm_batch.txt的文本文件中输入命令。
在Tools菜单中选择Run Batch进行批量处理。
7 设置
目前，运行SDM仅需指定一个参数，该参数用于在阈值化处理后自动使用MRIcron查看结果。
7.1 设置首选项
运行SDM-PSI时可指定五个参数（其中两个必填）: - The brain viewer：用于在阈值化处理后自动查看结果 - 核心二进制文件路径 - SDM-PSI MASK和模板路径 - 软件自动更新参数 - 多线程值
7.2 Brain viewer
你可以禁用brain viewer，或通过在Tools菜单中选择Preferences打开下面对话框来指定你的MRIcron路径：
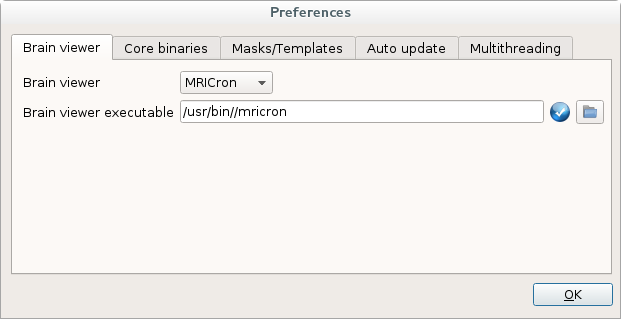
MRIcron可以点击这里下载。
7.3 核心二进制文件路径
为了进行运算，SdmPsiGui需要知道从哪获得SdmPsi的核心二进制文件（sdm_parse，sdm_core和imgcalc）。默认情况下，软件会在用户下载的SdmPsiGui文件夹内搜索这些文件。因此，除非用户需要使用特定版本的核心二进制文件（例如为特定需求提供的定制版本），否则无需担心此参数的设置。
如果用户需要指定位置，可以在Tools菜单中选择Preferences并选择Core binaries选项卡：
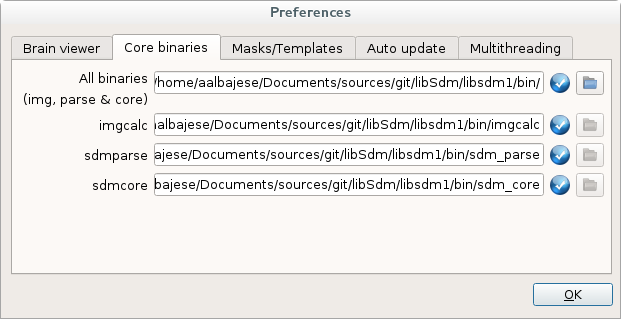
包含核心二进制文件的文件夹可通过以下方式指定：点击All binaries对应的文件夹图标按钮，然后导航至目标文件夹。
7.4 MASK或模板路径
与核心二进制文件类似，SdmPsiGui需要知道SdmPsi的MASK、模板和其他数据文件的存储位置。同样，与核心二进制文件的情况一样，仅在非常特殊的情况下用户才需要指定不同的路径。这可以通过Preferences窗口的Masks/Templates选项卡完成。
7.5 自动升级
SdmPsiGui提供自动更新功能，当新版本可用时会自动更新。你可以在Auto update选项卡中启用此功能。如果需要通过代理服务器建立http连接，也可以在此处设置代理服务器。
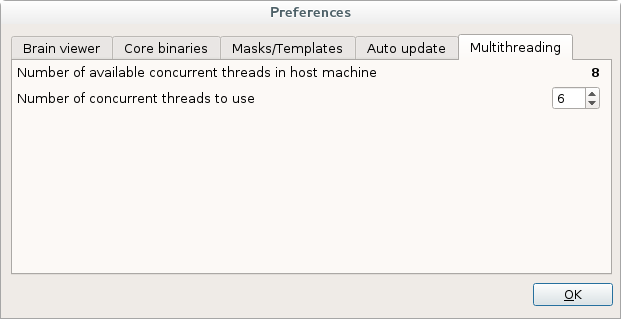
7.6 多线程
SdmPsi中最耗时的步骤已通过并行CPU线程的并行运算进行编码。在Multithreading选项卡中，用户可以查看其电脑提供的可用线程数，并选择要用多少线程数。虽然可以选择超过可用数量的线程，但不建议这样做，因为性能可能会下降。此外，如果需要在SdmPsi运算时使用电脑，建议至少预留一个线程。
8 如何引用
我们投入了大量的时间和精力来创造SDM，请在使用它进行元分析时引用它。
请使用下列参考文献（在合适的情况下）:
8.1 介绍voxel-based meta-analyses
Radua & Mataix-Cols (2012)
Müller et al. (2018)
8.2 SDM方法
First method (SDM)：Radua & Mataix-Cols (2009)
Meta-comparisons：Radua et al. (2010)
Effect sizes (ES-SDM)：Radua et al. (2012)
Anisotropic kernels (AES-SDM)：Radua, Rubia, et al. (2014)
之前方法的问题空间收敛性检验：Albajes-Eizagirre & Radua (2018)
当前方法的主要论文Permutation of subject images (SDM-PSI)：Albajes-Eizagirre, Solanes, Vieta, et al. (2019)
8.3 SDM的特定白质，TBSS和FreeSurfer模板
白质：Radua et al. (2011)
Fractional anistropy (TBSS)：Peters et al. (2012)
Cortical thickness (FreeSurfer)：Li et al. (2020)
8.4 改进的图谱
Radua, Grau, et al. (2014)
De Schotten et al. (2011)
Thiebaut de Schotten et al. (2011)
9 论坛
报告SDM软件中的问题和解决方案。
参考文献
Albajes-Eizagirre, A., & Radua, J. (2018). What do results from coordinate-based meta-analyses tell us? Neuroimage, 176, 550–553. https://doi.org/10.1016/j.neuroimage.2018.04.065
Albajes-Eizagirre, A., Solanes, A., Fullana, M. A., Ioannidis, J. P. A., Fusar-Poli, P., Torrent, C., Solé, B., Bonnín, C. M., Vieta, E., Mataix-Cols, D., & Radua, J. (2019). Meta-analysis of voxel-based neuroimaging studies using seed-based d mapping with permutation of subject images (SDM-PSI). Journal of Visualized Experiments, 153. https://doi.org/10.3791/59841
Albajes-Eizagirre, A., Solanes, A., & Radua, J. (2019). Meta-analysis of non-statistically significant unreported effects. Statistical Methods in Medical Research, 28(12), 3741–3754. https://doi.org/10.1177/0962280218811349
Albajes-Eizagirre, A., Solanes, A., Vieta, E., & Radua, J. (2019). Voxel-based meta-analysis via permutation of subject images (PSI): Theory and implementation for SDM. Neuroimage, 186, 174–184. https://doi.org/10.1016/j.neuroimage.2018.10.077
De Schotten, M. T., Dell’acqua, F., Forkel, S. J., Simmons, A., Vergani, F., Murphy, D. G. M., & Catani, M. (2011). A lateralized brain network for visuospatial attention. Nature Neuroscience, 14(10), 1245–1246. https://doi.org/10.1038/nn.2905
Hedges, L. V., & Olkin, I. (1985). Statistical methods for meta-analysis [Book]. Academic Press.
Li, Q., Zhao, Y. J., Chen, Z. Q., Long, J. Y., Dai, J., Huang, X. Q., Lui, S., Radua, J., Vieta, E., Kemp, G. J., Sweeney, J. A., Li, F., & Gong, Q. Y. (2020). Meta-analysis of cortical thickness abnormalities in medication-free patients with major depressive disorder. Neuropsychopharmacology, 45(4), 703–712. https://doi.org/10.1038/s41386-019-0563-9
Müller, V. I., Cieslik, E. C., Laird, A. R., Fox, P. T., Radua, J., Mataix-Cols, D., Tench, C. R., Yarkoni, T., Nichols, T. E., Turkeltaub, P. E., Wager, T. D., & Eickhoff, S. B. (2018). Ten simple rules for neuroimaging meta-analysis. Neuroscience and Biobehavioral Reviews, 84, 151–161. https://doi.org/10.1016/j.neubiorev.2017.11.012
Peters, B. D., Szeszko, P. R., Radua, J., Ikuta, T., Gruner, P., DeRosse, P., Zhang, J. P., Giorgio, A., Qiu, D. Q., Tapert, S. F., Brauer, J., Asato, M. R., Khong, P. L., James, A. C., Gallego, J. A., & Malhotra, A. K. (2012). White matter development in adolescence: Diffusion tensor imaging and meta-analytic results. Schizophrenia Bulletin, 38(6), 1308–1317. https://doi.org/10.1093/schbul/sbs054
Radua, J., Grau, M., Heuvel, O. A. van den, Thiebaut de Schotten, M., Stein, D. J., Canales-Rodríguez, E. J., Catani, M., & Mataix-Cols, D. (2014). Multimodal voxel-based meta-analysis of white matter abnormalities in obsessive-compulsive disorder. Neuropsychopharmacology, 39(7), 1547–1557. https://doi.org/10.1038/npp.2014.5
Radua, J., Heuvel, O. A. van den, Surguladze, S., & Mataix-Cols, D. (2010). Meta-analytical comparison of voxel-based morphometry studies in obsessive-compulsive disorder vs other anxiety disorders. Archives of General Psychiatry, 67(7), 701–711. https://doi.org/10.1001/archgenpsychiatry.2010.70
Radua, J., & Mataix-Cols, D. (2009). Voxel-wise meta-analysis of grey matter changes in obsessive-compulsive disorder. British Journal of Psychiatry, 195(5), 393–402. https://doi.org/10.1192/bjp.bp.108.055046
Radua, J., & Mataix-Cols, D. (2012). Meta-analytic methods for neuroimaging data explained. Biology of Mood & Anxiety Disorders, 2, 6. https://doi.org/10.1186/2045-5380-2-6
Radua, J., Mataix-Cols, D., Phillips, M. L., El-Hage, W., Kronhaus, D. M., Cardoner, N., & Surguladze, S. (2012). A new meta-analytic method for neuroimaging studies that combines reported peak coordinates and statistical parametric maps. European Psychiatry, 27(8), 605–611. https://doi.org/10.1016/j.eurpsy.2011.04.001
Radua, J., Rubia, K., Canales, E. J., Pomarol-Clotet, E., Fusar-Poli, P., & Mataix-Cols, D. (2014). Anisotropic kernels for coordinate-based meta-analyses of neuroimaging studies. Frontiers in Psychiatry, 5. https://doi.org/10.3389/fpsyt.2014.00013
Radua, J., Via, E., Catani, M., & Mataix-Cols, D. (2011). Voxel-based meta-analysis of regional white-matter volume differences in autism spectrum disorder versus healthy controls. Psychological Medicine, 41(7), 1539–1550. https://doi.org/10.1017/s0033291710002187
Rojkova, K., Volle, E., Urbanski, M., Humbert, F., Dell’Acqua, F., & Thiebaut de Schotten, M. (2016). Atlasing the frontal lobe connections and their variability due to age and education: A spherical deconvolution tractography study [Journal Article]. Brain Structure and Function, 221(3), 1751–1766. https://doi.org/10.1007/s00429-015-1001-3
Smith, S. M., & Nichols, T. E. (2009). Threshold-free cluster enhancement: Addressing problems of smoothing, threshold dependence and localisation in cluster inference. NeuroImage, 44(1), 83–98. https://doi.org/10.1016/j.neuroimage.2008.03.061
Thiebaut de Schotten, M., ffytche, D. H., Bizzi, A., Dell’Acqua, F., Allin, M., Walshe, M., Murray, R., Williams, S. C., Murphy, D. G. M., & Catani, M. (2011). Atlasing location, asymmetry and inter-subject variability of white matter tracts in the human brain with MR diffusion tractography. NeuroImage, 54(1), 49–59. https://doi.org/10.1016/j.neuroimage.2010.07.055
Winkler, A. M., Ridgway, G. R., Webster, M. A., Smith, S. M., & Nichols, T. E. (2014). Permutation inference for the general linear model. NeuroImage, 92, 381–397. https://doi.org/10.1016/j.neuroimage.2014.01.060